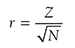When making group comparisons when the distributional assumption of the independent samples t-test is violated, the nonparametric counterparts, the Wilcoxon rank-sum test and the MannμWhitney test, should be used. Let us consider an example where we compare family satisfaction with dementia care between a traditional caregiver group (N = 13) and a music therapy group (N = 9). We know that because these sample sizes are small the distribution will not be normal; therefore, either the Wilcoxon rank-sum test or the MannμWhitney test will be appropriate for this situation instead of the independent samples t-test. The data are shown in Table 13-1.
Traditional Caregiver Group | Music Therapy Group |
|---|---|
1 | 21 |
12 | 25 |
17 | 29 |
15 | 27 |
9 | 9 |
15 | 15 |
17 | 27 |
19 | 19 |
13 | 16 |
7 | |
16 | |
3 | |
14 |
Note: numbers represents Family Satisfaction and the scale (0-30)
As these are nonparametric tests, there are no distributional assumptions. However, these tests do assume the following:
- Random sample
- Two groups are independent of each other
- Level of measurements is at least ordinal
First, we need to set up hypotheses; these are similar to those of an independent samples t-test:
H0: The distributional functions are identical for two groups.
Ha: The distributional functions are not identical for two groups.
The test statistics for both tests are calculated using ranks of the data. When the group sample sizes are equal, the test statistic is the summed rank value that is the smallest. However, it will be the summed rank value of the group with the smaller sample size if the group sample sizes are not equal. For our example, the sum of rank value in the traditional caregiver group is 109.50, and that in the music therapy group is 143.50. Because of the unequal sample sizes, our test statistic is the summed rank value for the music therapy group, as it is the smaller sample.
Once the statistic is computed, the associated p-value is evaluated, and we make the decision to reject or not reject the null hypothesis (i.e., reject the null hypothesis when the p-value associated with the computed statistic is small, or not reject when the p-value associated with the computed statistic is large).
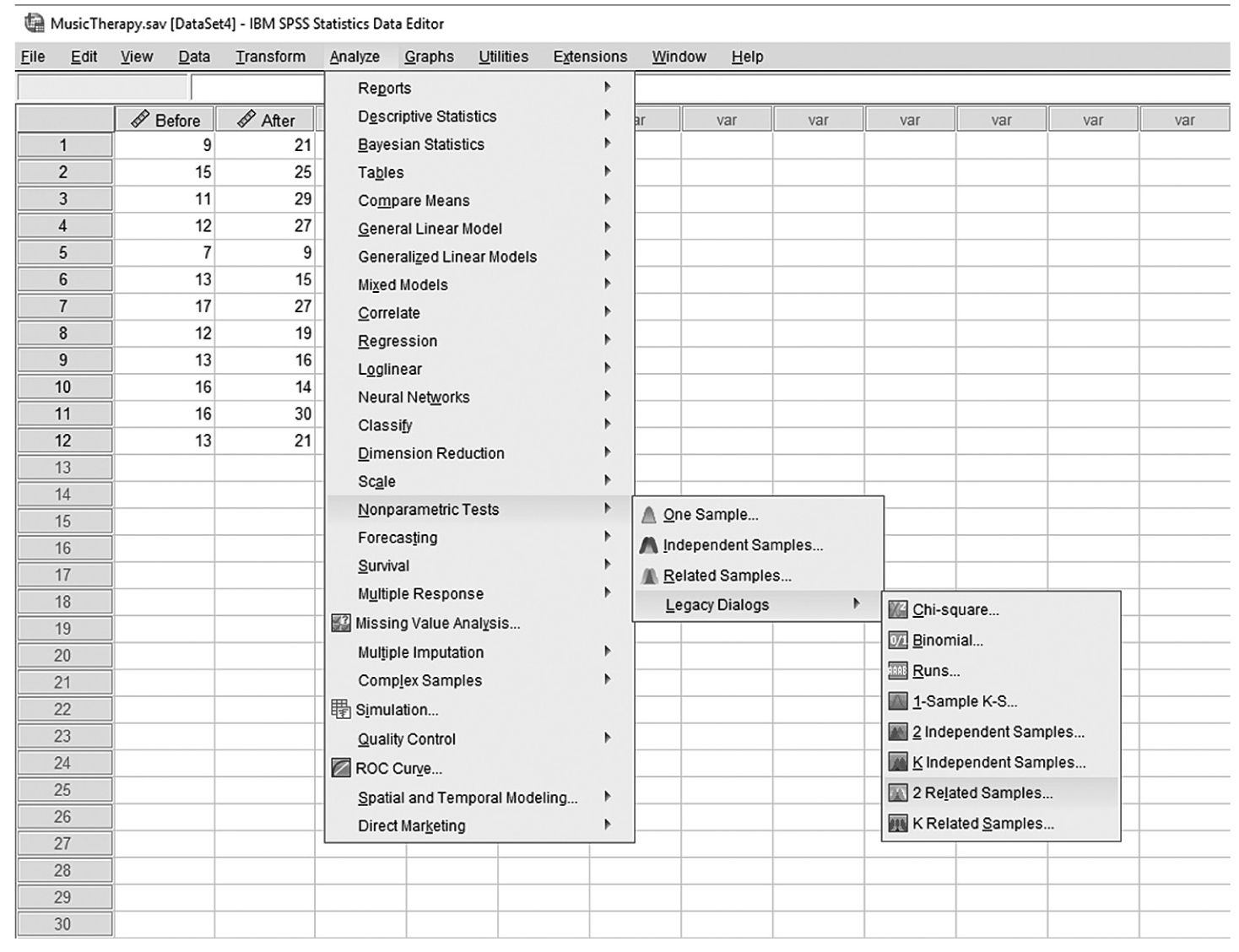
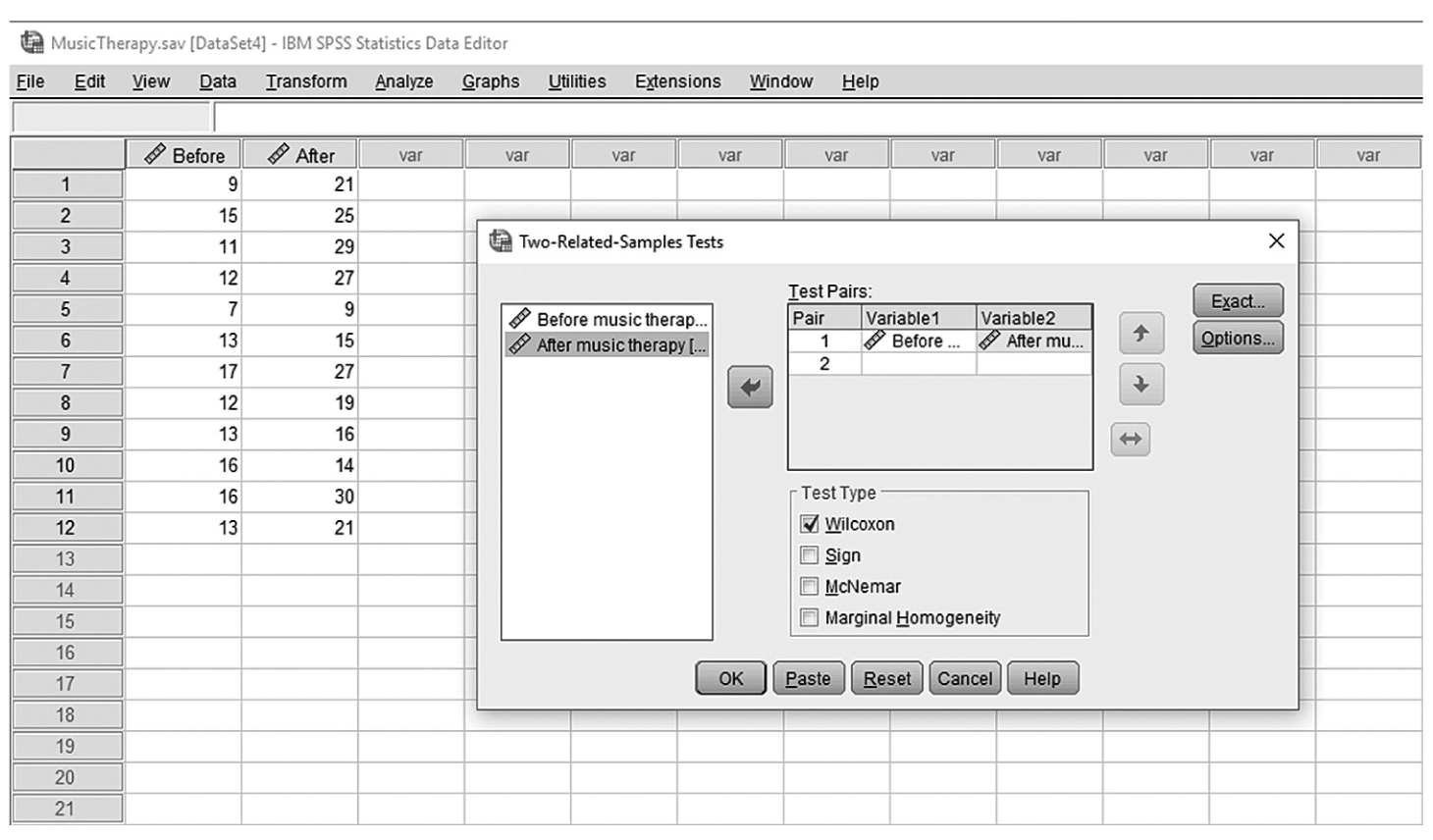
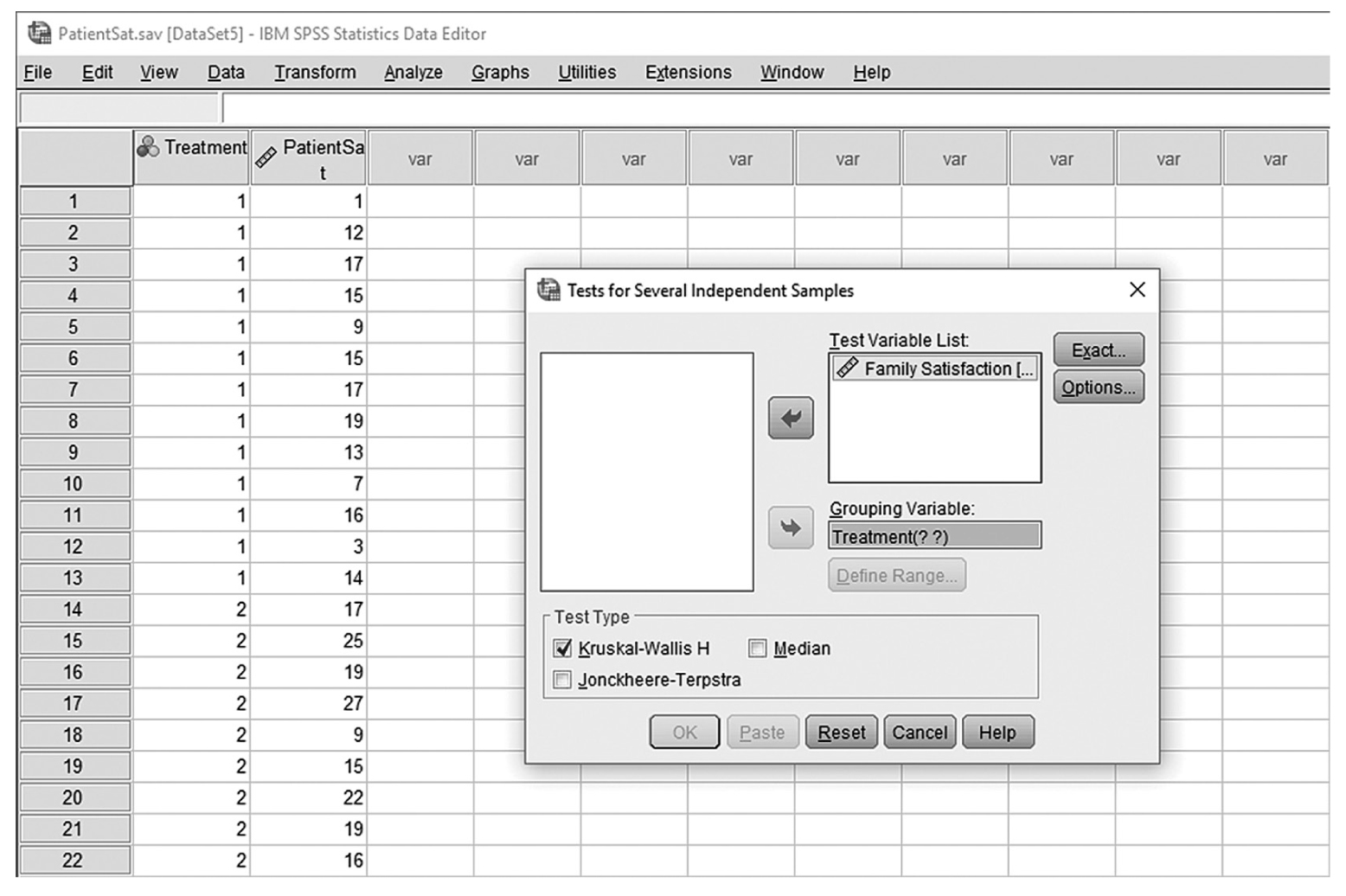
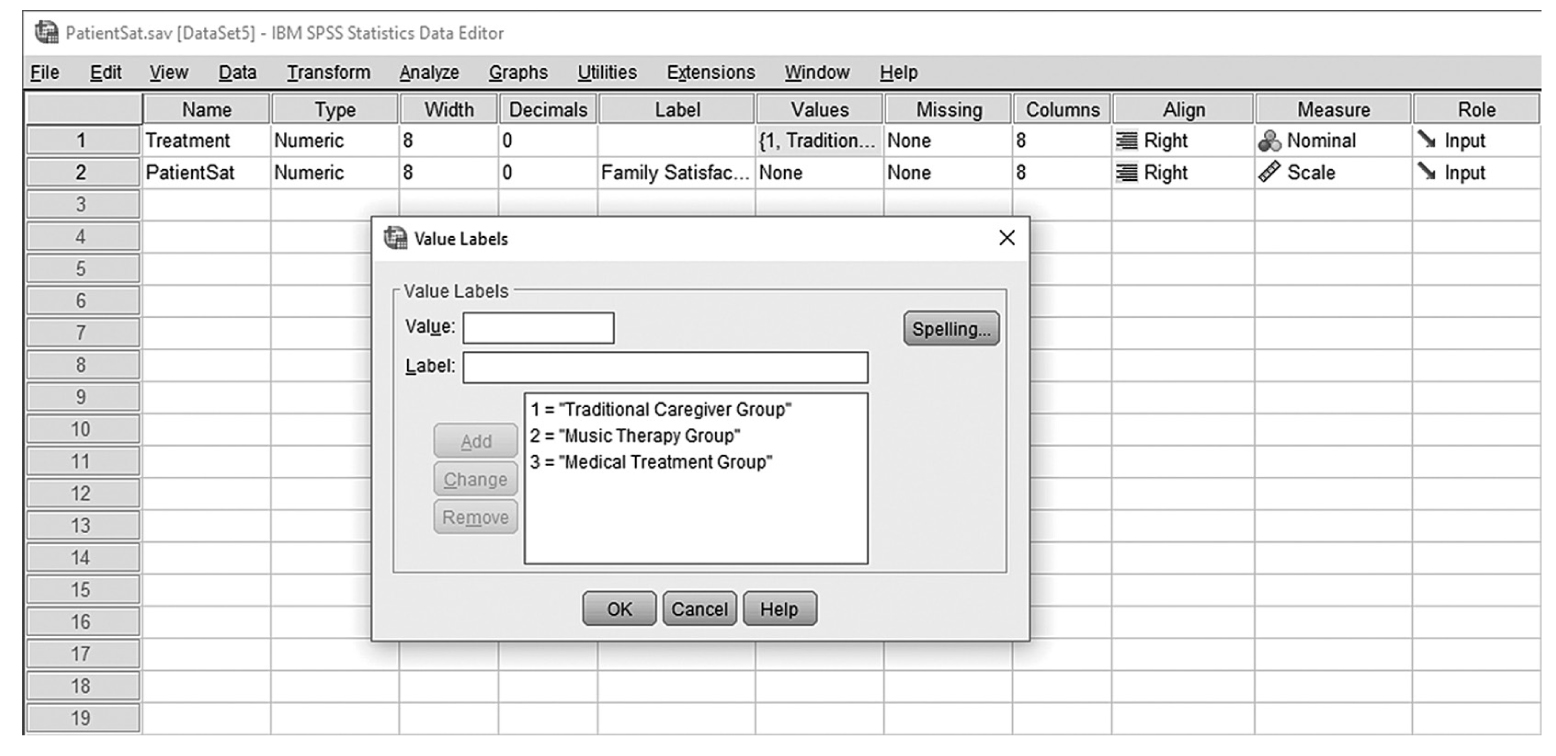
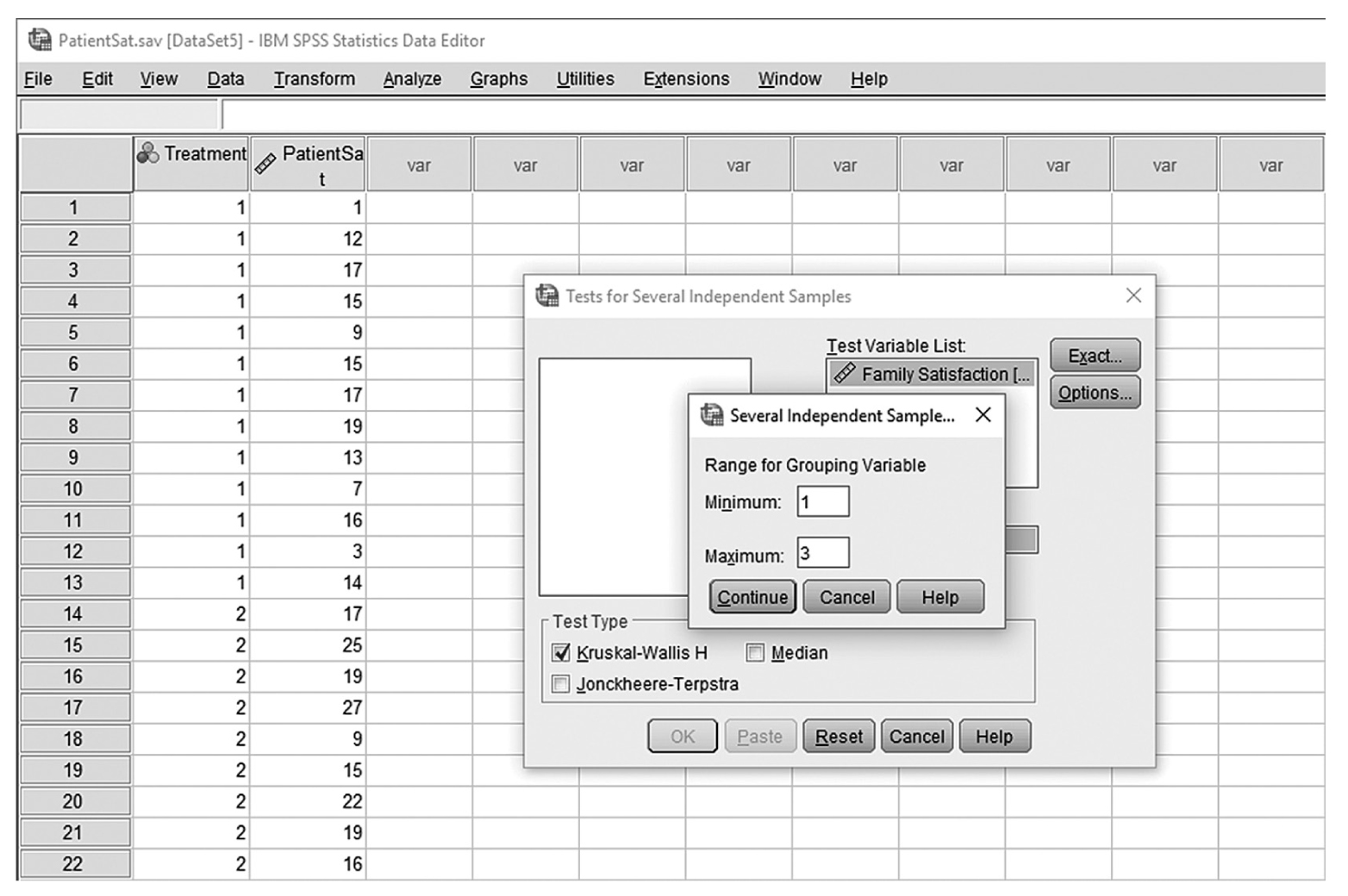
To conduct Wilcoxon rank-sum tests and/or MannμWhitney tests in IBM SPSS Statistics software (SPSS), you will open FamilySat.sav and go to Analyze > Nonparametric Tests > Legacy Dialogs > 2 Independent Samples, as shown in Figure 13-1. In the Two Independent Samples Tests dialog box, move the dependent variable, family satisfaction (“FamilySat”), into “Test Variable List,” and the independent variable, “Treatment,” into “Grouping Variable” by clicking the corresponding arrow buttons in the middle (Figure 13-2). You will notice that “MannμWhitney U” is checked by default under “Test Type”; this option will produce statistics of both Wilcoxon rank-sum tests and MannμWhitney tests. You will also notice that the “OK” button is not active because we have not yet defined our two groups. As you see in Figure 13-3, we have defined the coding of 1 for the traditional caregiver group and 2 for the music therapy group. Now click on the “Define Groups” button and assign 1 for group 1 and 2 for group 2, as in Figure 13-4. Clicking “Continue” and then “OK” will produce the output. The example output is shown in Table 13-2.
Selecting MannμWhitney tests in SPSS.
A screenshot in S P S S shows selection of the Analyze menu, with Nonparametric tests command chosen, from which Legacy Dialogs is selected, under which 2 Independent Samples option is selected. Data in the worksheet shows columns of numerical data.
Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. “IBM SPSS Statistics software (“SPSS”)”. IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.
Defining variables in MannμWhitney tests in SPSS.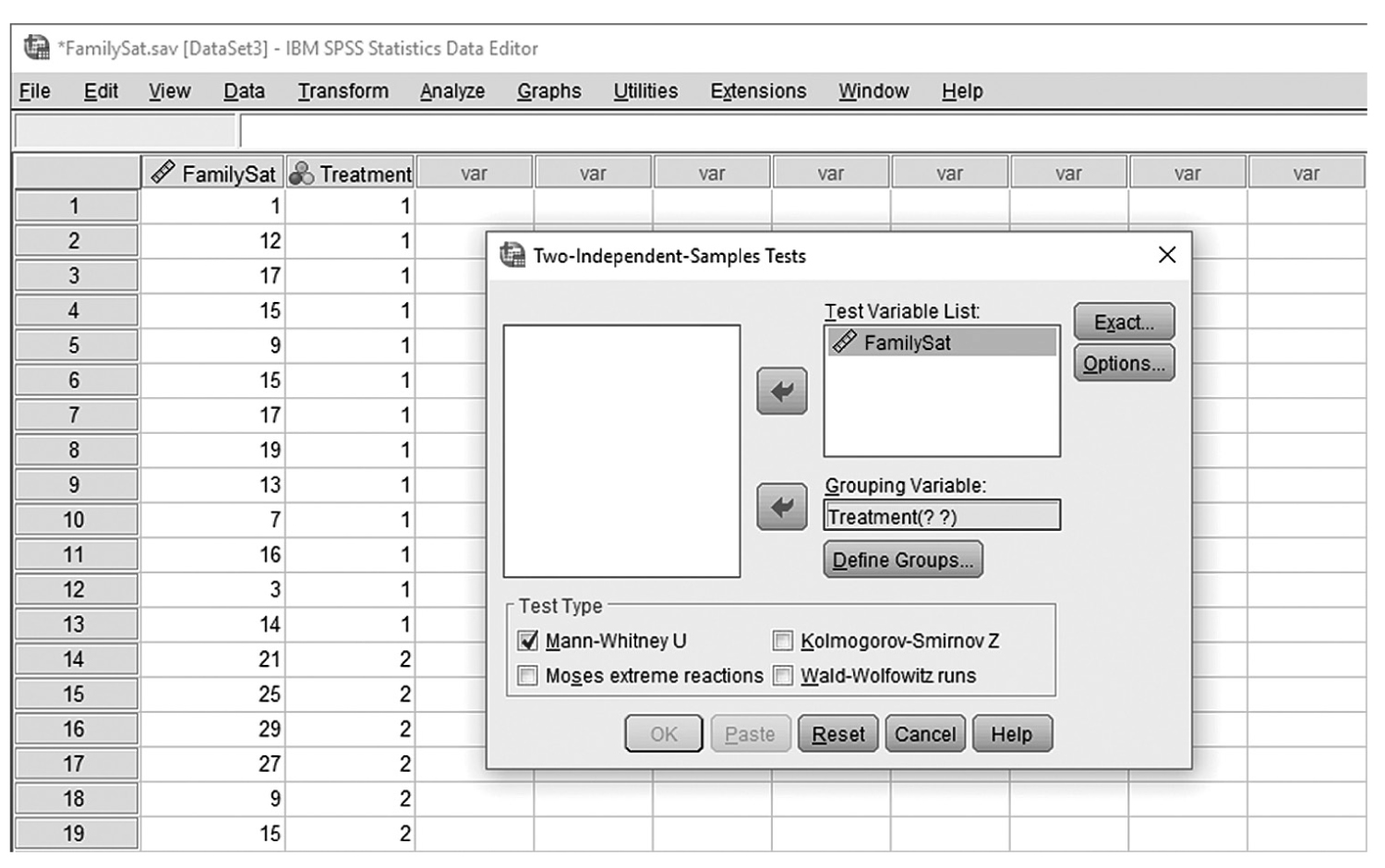
A screenshot in S P S S Editor defines variables in MannμWhitney Tests. The data in the worksheet shows columns of numerical data.
Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. “IBM SPSS Statistics software (“SPSS”)”. IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.
Coding scheme for the “Treatment” variable.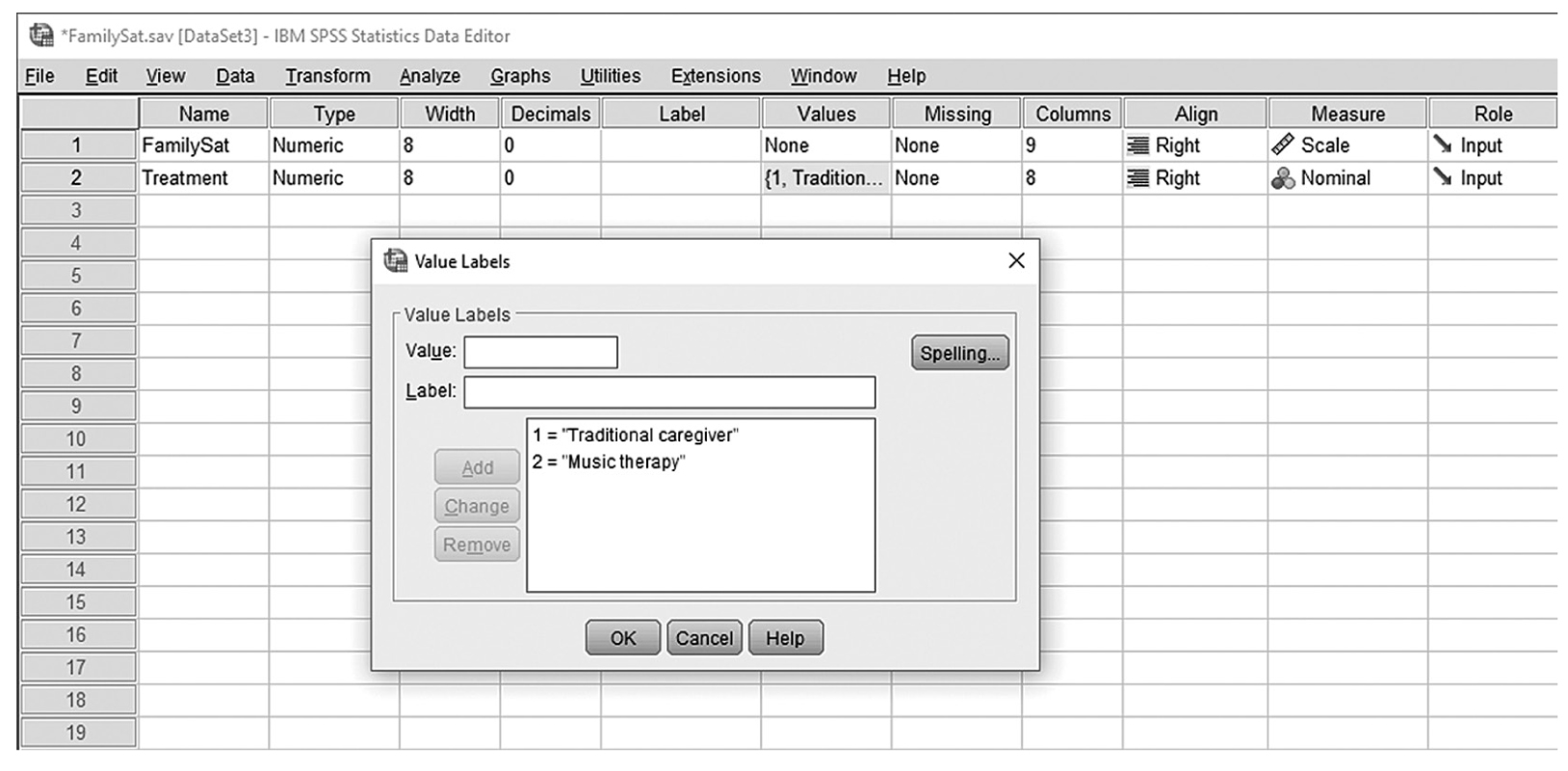
A screenshot in S P S S depicts the coding scheme for the variable, Treatment.
Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. “IBM SPSS Statistics software (“SPSS”)”. IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.
Defining groups in MannμWhitney tests in SPSS.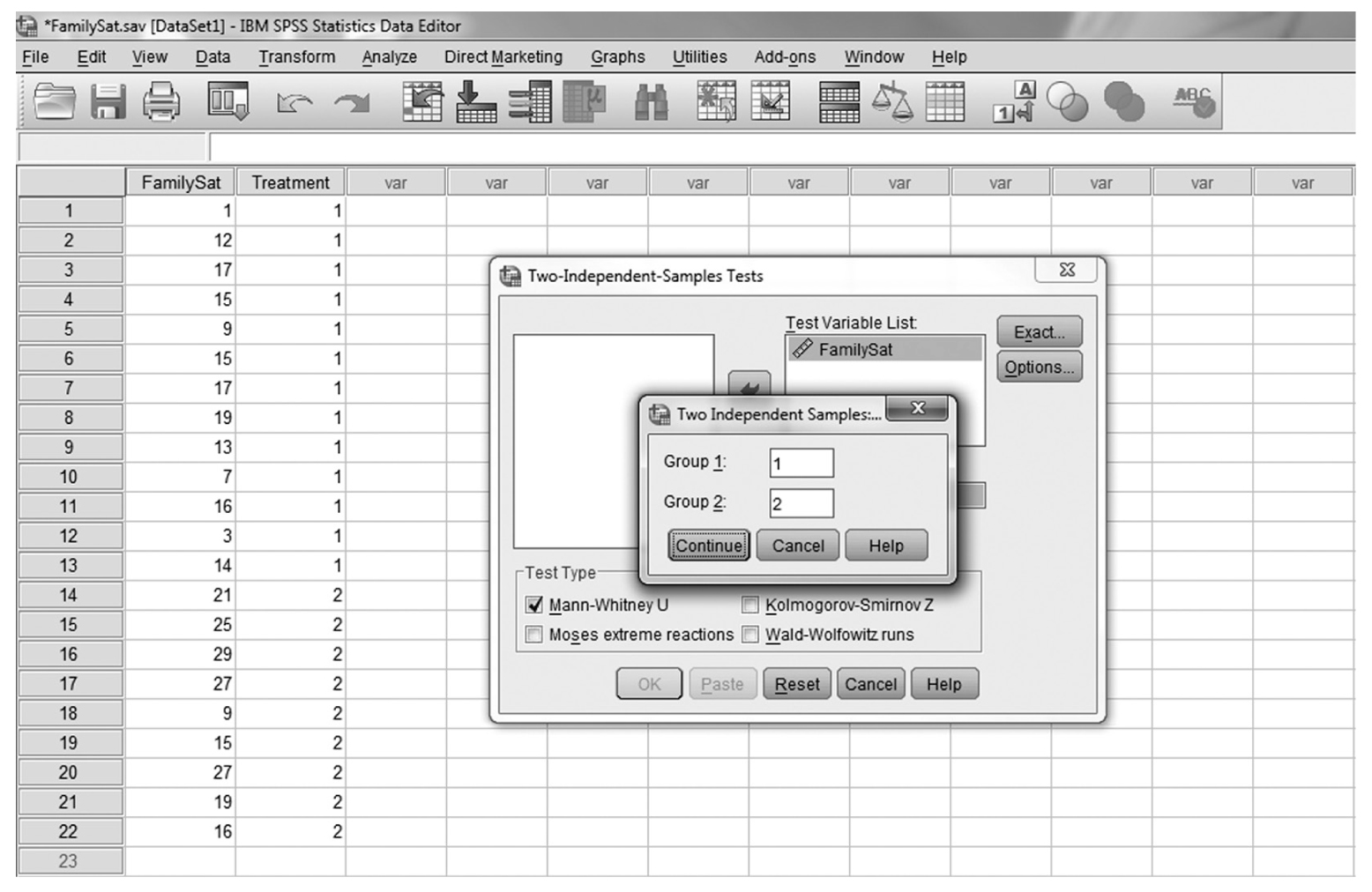
A screenshot in S P S S shows a dialog box, where groups are defined in a two-independent samples t-test. There are two columns, FamilySat and Treatment, with rows of numerical data under each column.
Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. “IBM SPSS Statistics software (“SPSS”)”. IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.
Ranks | ||||
|---|---|---|---|---|
Treatment | N | Mean Rank | Sum of Ranks | |
FamilySat | Traditional caregiver | 13 | 8.42 | 109.50 |
Music therapy | 9 | 15.94 | 143.50 | |
Total | 22 | |||
Test Statisticsb | |
|---|---|
FamilySat | |
MannμWhitney U | 18.500 |
Wilcoxon W | 109.500 |
Z | μ2.678 |
Asymp. sig. (two-tailed) | .007 |
Exact sig. [2 × (one-tailed sig.)] | .006a |
aNot corrected for ties
bGrouping variable: treatment
When reporting MannμWhitney test results, you should report the size of the corresponding statistics and associated p-value as well as medians of groups, so that the readers will know how the sample statistics are different. Effect size, r, can be computed and reported with the following equation:
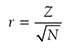
where Z is one of the statistics that SPSS calculates for MannμWhitney tests and N is the total number of observations. The following are examples of how to report the test results.
- For MannμWhitney tests: Family satisfaction levels in the traditional caregiver group (Mdn = 14.00) did differ substantially from the music therapy group (Mdn = 21.00), U = 18.50, z = -2.68, p = .007, r =-.57.
- For Wilcoxon rank-sum tests: Family satisfaction levels in the traditional caregiver group (Mdn = 14.00) differed substantially from the music therapy group (Mdn = 21.00), Ws = 109.50, z = -2.68, p = .007, r = -.57.
With a p-value of .007, we can see that family satisfaction differs substantially depending upon the type of treatment, and the group who received music therapy had substantially higher satisfaction than the group who received traditional care based on the descriptive statistics. Note that the median is and should be reported as a better measure of central tendency for nonparametric tests with no distributional assumption. You may compute the median as discussed in Chapter 6.