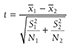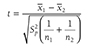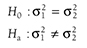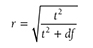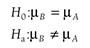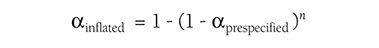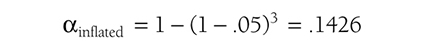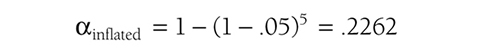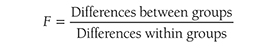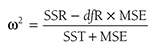section name header

Learning Objectives ⬇

The principal goals of this chapter are to help you understand the purpose of statistical tests of differences between means (difference tests), when to use these tests, how the tests are computed, and how to interpret the results. This chapter will prepare you to:

Key Terms ⬆ ⬇

Introduction ⬆ ⬇

We use tests of mean differences to make comparisons. In health care, we are often interested in comparing one group to another or comparing treatments to determine which is more effective. Such analyses may be found in descriptive comparative or experimental investigations. For example, in a descriptive comparative investigation, we may ask how cancer incidence varies depending on sex or gender. To be more specific, we might ask, “Does the mean number of new cases of lung cancer each year differ by sex?” Descriptive comparative studies help to explain phenomena that occur naturally without the researcher influencing any variables.

CASE STUDY
Kurnat-Thoma, E., Edwards, V., & Emery, K. (2018). Axillary, Tympanic, and Temporal Thermometry Comparison in a Community Hospital Pediatric Unit. Pediatric Nursing, 44(5), 235-246.

In 2018, Kurnat-Thoma, Edwards, and Emery published their findings from a prospective study that evaluated the accuracy of a temporal scanner (the Exergen Temporal Scanner (TAT)-5000) compared with axillary or tympanic temperature measurement in hospitalized pediatric patients. The study ideas originated from bedside nurses on a research committee who were concerned with the reliability and accuracy of tympanic temperature readings. A convenience sample of all pediatric patients admitted except for preterm infants (n = 140) was obtained from a 187-bed community hospital in the Washington, DC, metropolitan area. Because all patients’ temperatures were measured in both ways, they were their own controls.

Kurnat-Thoma, Edwards, and Emery conducted dependent t-tests to determine if there were differences on average temperature readings between different thermometry methods (i.e., axillary or tympanic versus temporal). The researchers reported a dependent t-test because they were comparing one group (all patients) on two different noninvasive temperature measures. They also conducted an independent samples t-test to determine if there were differences between temperature readings in two distinct groups, child and adolescent patients, measured on day shift versus night shift.

The researchers discovered that there were substantial differences between mean temperature readings from two different thermometry methods in all of the newborn, child, and adolescent groups. Additionally, there were substantial differences between child and adolescent groups on the day and night shifts. They presented their findings in the table that follows.

Range (˚F)

Mean

SD

n

t

df

p

Outcome Temperaturea

Ambient Room

67.80μ85.10

75.00

3.03

139

Axillary

96.50μ101.30

98.12

0.94

59

Tympanic

95.00μ103.00

98.06

1.53

77

Temporal Artery

97.10μ105.50

99.15

1.17

139

0μ3 Monthsb

μ9.33

52

0.001*

Axillary

98.06

0.81

53

Temporal Artery

98.92

0.77

53

3 Monthsμ21 Yearsb

μ11.28

72

.001*

Tympanic

98.06

1.57

73

Temporal Artery

99.31

1.35

73

3 Months-21 Years

Tympanic Day Shift

98.52

1.67

45

μ3.40

71

0.001*

Tympanic Night Shift

97.33

1.06

29

Temporal Artery Day Shift

99.56

1.59

52

μ2.63

78

0.01*

Temporal Artery Night Shift

98.87

0.75

29

aAxillary plus tympanic sample size is n = 136 because four study patients had oral and rectal measurements that were removed from analysis.

bTemperature outcomes without a corresponding paired measure were removed from analysis; therefore, there was a slight decrease in sample size.

Notes. Sample size does not total 140 for ambient, TAT outcomes because of missing data.

*Bonferroni-corrected threshold is p≤ 0.01.

Reprinted from Kurnat-Thoma, E., Edwards, V., & Emery, K. (2018). Axillary, Tympanic, and Temporal Thermometry Comparison in a Community Hospital Pediatric Unit. Pediatric Nursing, 44(5), 235μ246. Reprinted with permission of the publisher, Jannetti Publications, Inc., East Holly Avenue/Box 56, Pitman, NJ 08071-0056; (856) 256-2300; FAX (856) 589-7463; Website: www.pediatricnursing.net; For a sample copy of the journal, please contact the publisher.

Kurnat-Thoma, Edwards, and Emery (2018) presents a good example of comparing differences between groups—in this case, noninvasive temperature readings between two different thermometry methods, and between day shift and night shift. Group comparisons can also be made among three or more groups.

We can also apply testing for substantial differences between means to experimental questions. Experimental designs are highly controlled so that the investigator can determine the effect of the independent variable on the dependent variable. We may want to know what treatment or intervention produces the best outcome, such as “On average, which wound care treatment reduces healing time the most?” In both of these examples, we must be able to calculate a mean value for the dependent variable in order to make comparisons between means; here, the average number of new cases of lung cancer each year and the average time for wound healing. These tests require that dependent variables be continuous or measured at the interval or ratio level. In this chapter, we will discuss several statistical tests that compare group means of a continuous variable(s).

One-Sample T-Test ⬆ ⬇

The t-test is the simplest statistic when we are comparing two means, and a one-sample t-test is the simplest t-test. A one-sample t-test compares the mean score of a sample on a continuous dependent variable to a known value, which is usually the population mean. For example, say that we take a sample of students from the university and compare their average IQ to a known average IQ for the university. If we want to find out whether the sample mean IQ differs from the average university IQ, a one-sample t-test will give us the answer.

There are three assumptions for a one-sample t-test:

Always remember to check these assumptions before you conduct the test as violations can limit scientific conclusions.

Doing and Interpreting a One-Sample t-Test

As with all hypotheses testing, we need to first set up the hypotheses:

H0: There is no difference between the sample mean and a known population mean.

Ha: There is a difference between the sample mean and a known population mean.

or

H0: μ= 120

Ha: μ≠120.

The test statistic for a one-sample t-test can be computed by using the following formula:

where

x

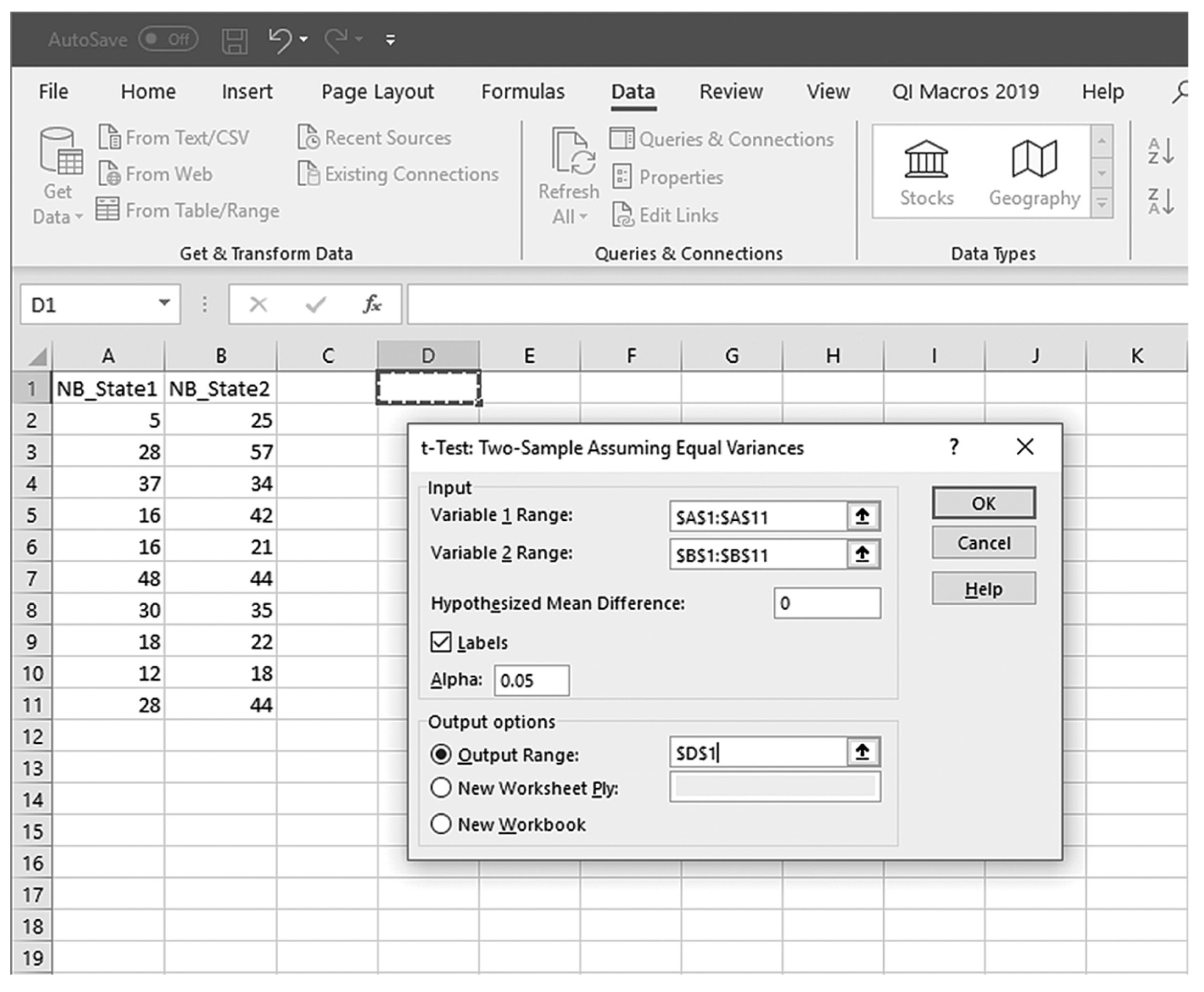
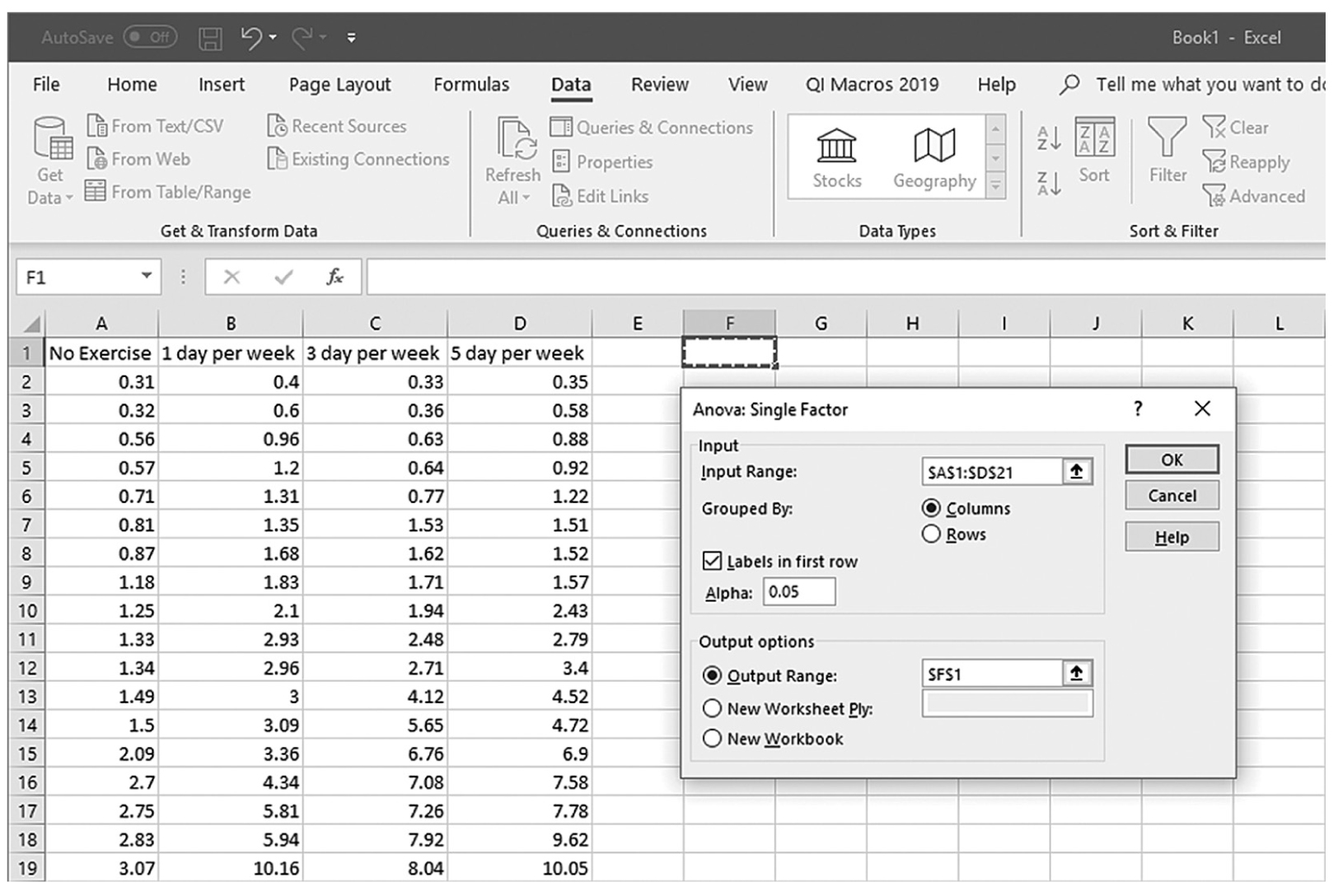
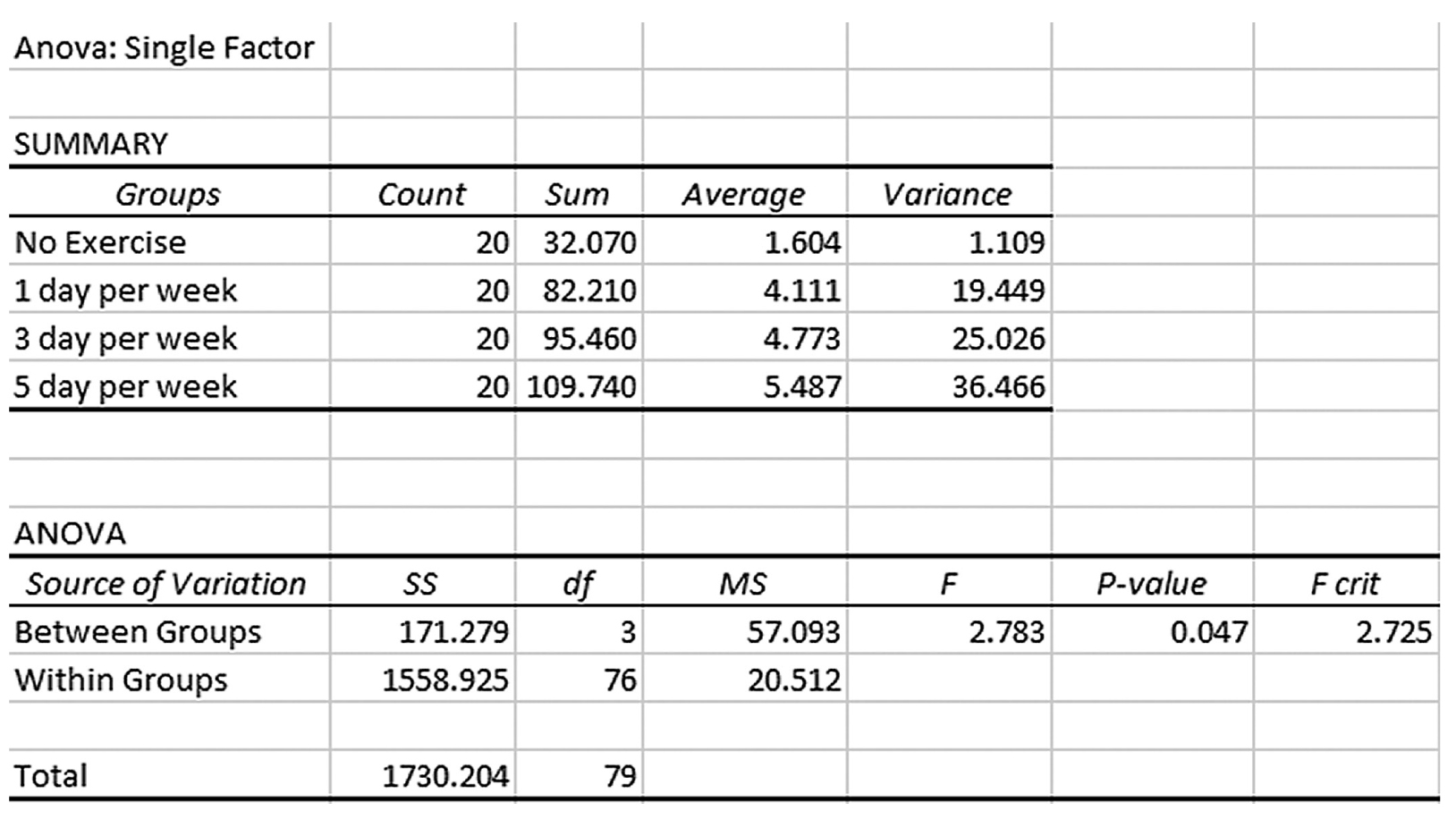
is the sample mean, μis the population mean, s is the sample standard deviation, and n is the sample size. Then we report the associated p-value with the computed statistic and support the p-value with a measure of effect size along with a corresponding interval estimate (i.e., confidence interval) as a measure of importance.

To conduct a one-sample t-test in Excel, you will open IQ.xlsx and go to Data > Data Analysis, as shown in Figure 11-1. Note that the list does not include one-sample t-test, but you can trick Excel and perform a one-sample t-test. First, you will type the word Average in cell B1, which is our label for a known population mean, and a known population mean, 120, in cells B2 and B3 (Figure 11-2). In the Data Analysis window, choose “t-Test: Two-Sample Assuming Unequal Variances” and then click “OK” (Figure 11-3). In the “t-Test: Two-Sample Assuming Unequal Variances” box, you will provide A1:A101 as Variable 1 Range and B1:B3 as Variable 2 Range with Labels selected (Figure 11-4). Clicking “OK” will then produce the output of the requested one-sample t-test; the example output is shown in Figure 11-5.

Finding Data Analysis ToolPak in Excel.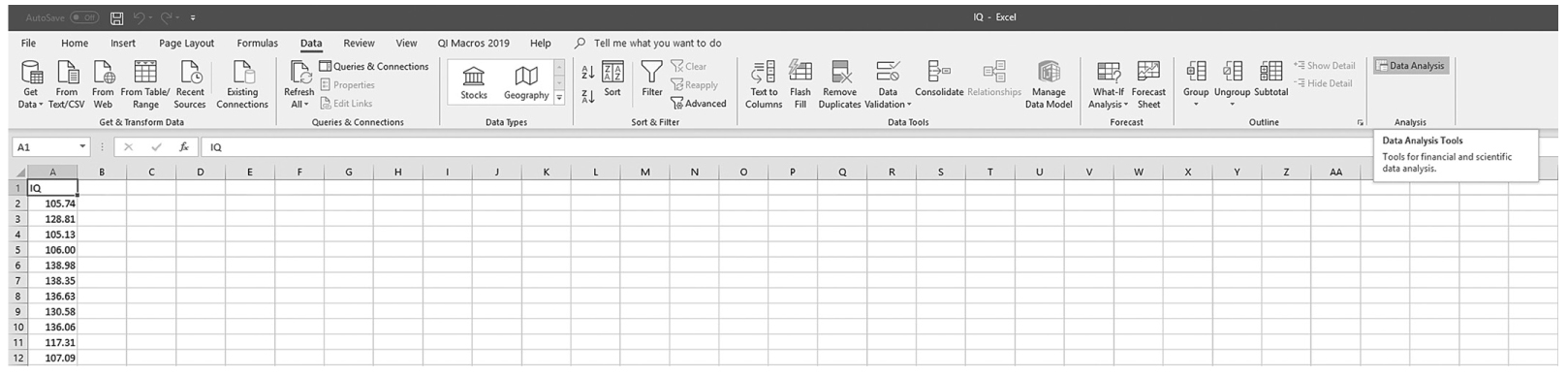

An Excel screenshot shows the Data Analysis ToolPak add-in, in the Analysis group under Data menu.

Courtesy of Microsoft Excel © Microsoft 2020.

Preparing the data for Excel to compute a one-sample t-test.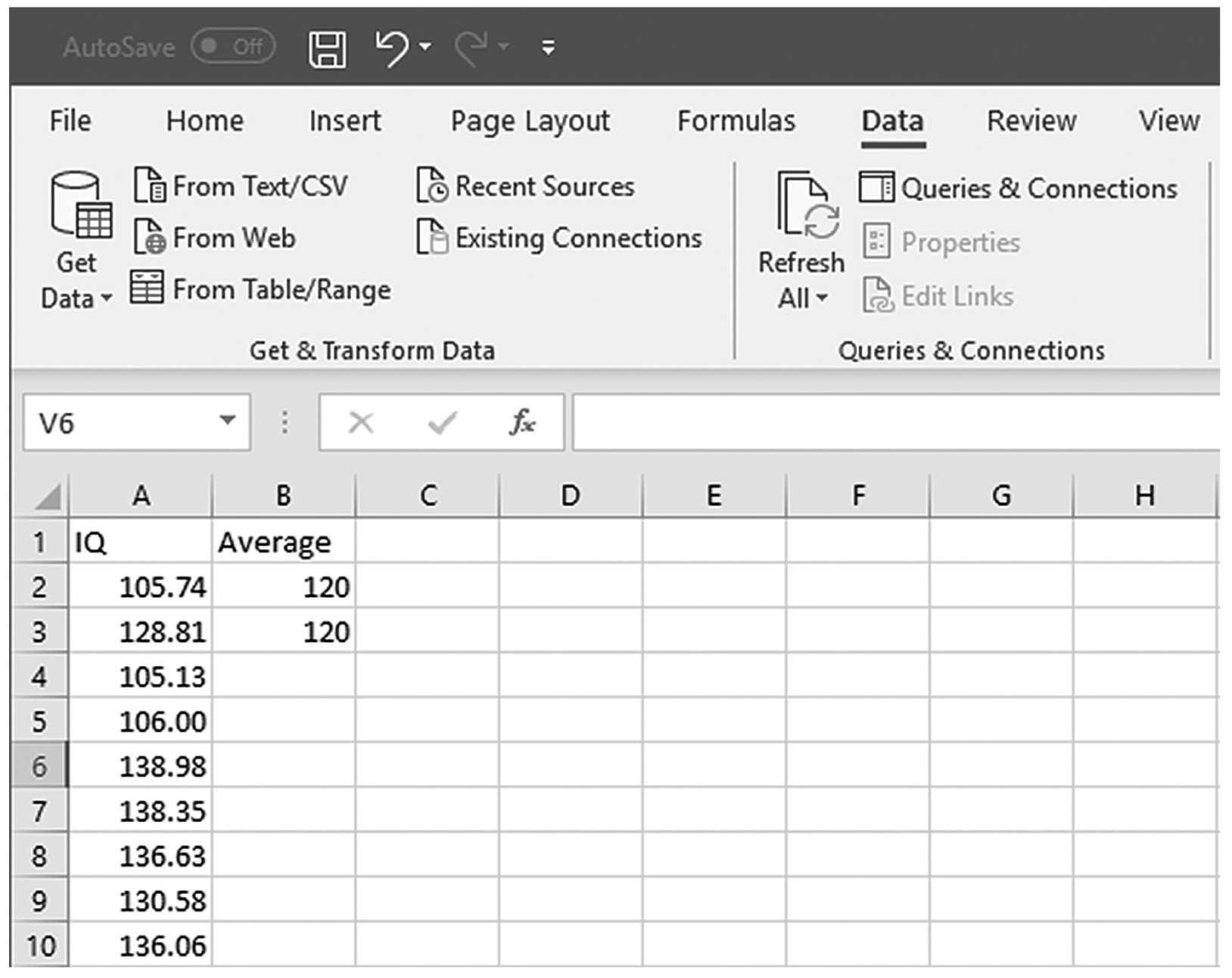

An Excel screenshot shows the column heading, I Q, in cell A 1, and numerical data entered in cells A 2 through A 10. The column heading, Average, is entered in cell B 1, and the value 120, entered in cells B 2 and B 3.

Courtesy of Microsoft Excel © Microsoft 2020.

Selecting a one-sample t-test within the Data Analysis ToolPak list in Excel.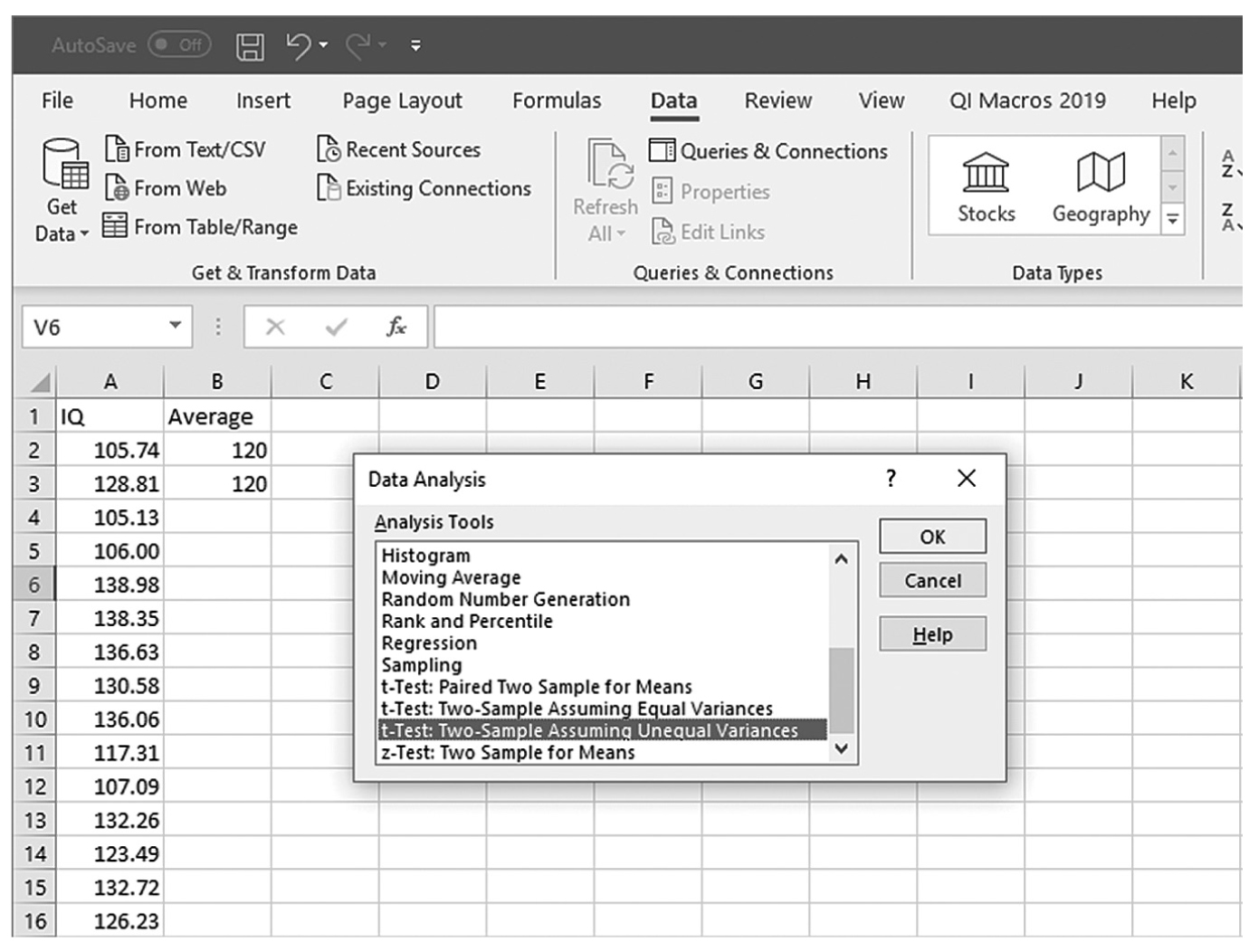

An Excel screenshot shows selection of the option, t-Test: Two-Sample Assuming Unequal Variances, within the Data Analysis ToolPak. The worksheet lists I Q with numerical data, and Average with the value 120 entered below it.

Courtesy of Microsoft Excel © Microsoft 2020.

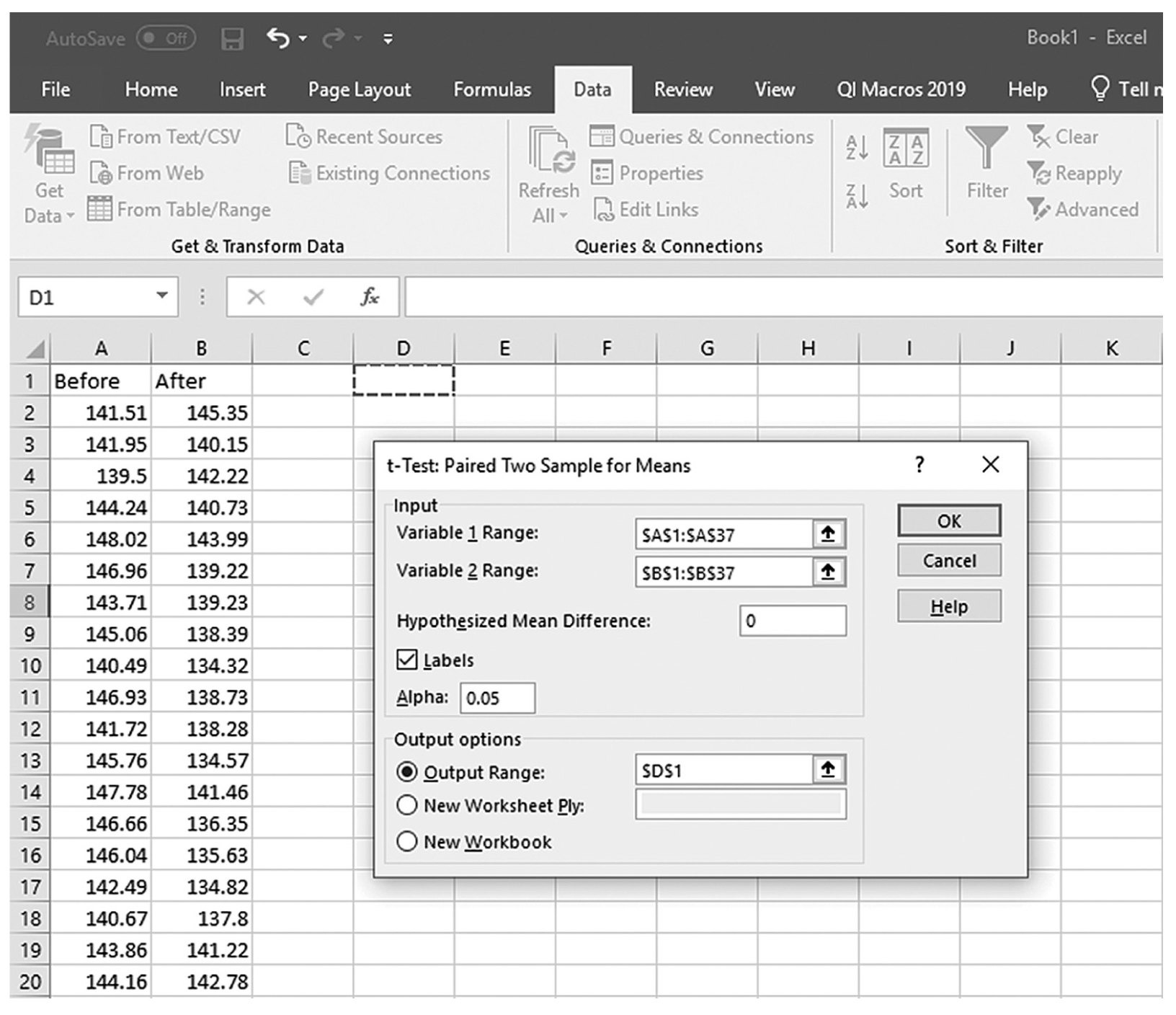
Defining data ranges and selecting options for a one-sample t-test in Excel.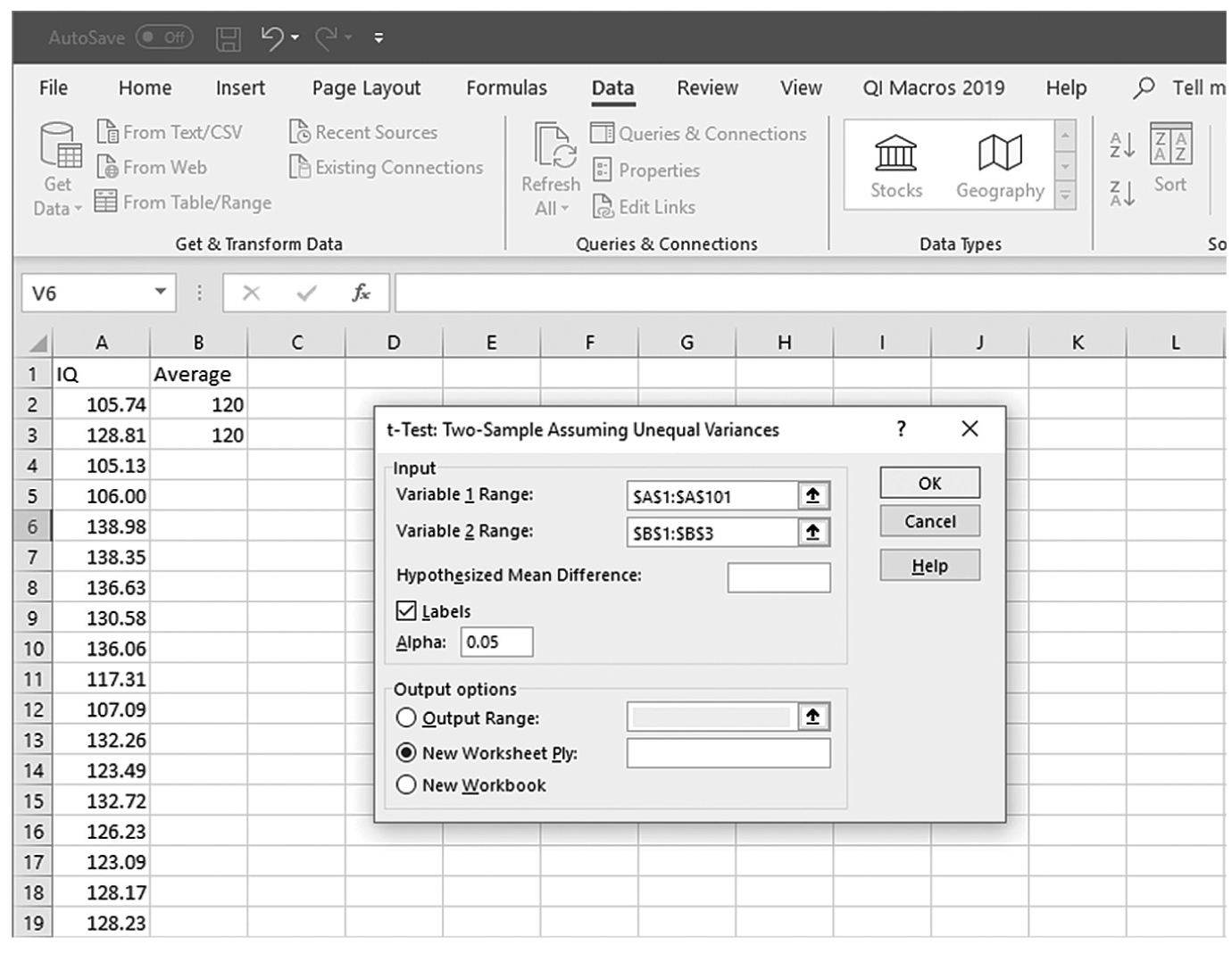

An Excel screenshot shows a dialog box with the inputting of data ranges and selecting output options for a one-sample t-test. The worksheet lists I Q with numerical data, and Average with the value 120 entered below it.

Courtesy of Microsoft Excel © Microsoft 2020.

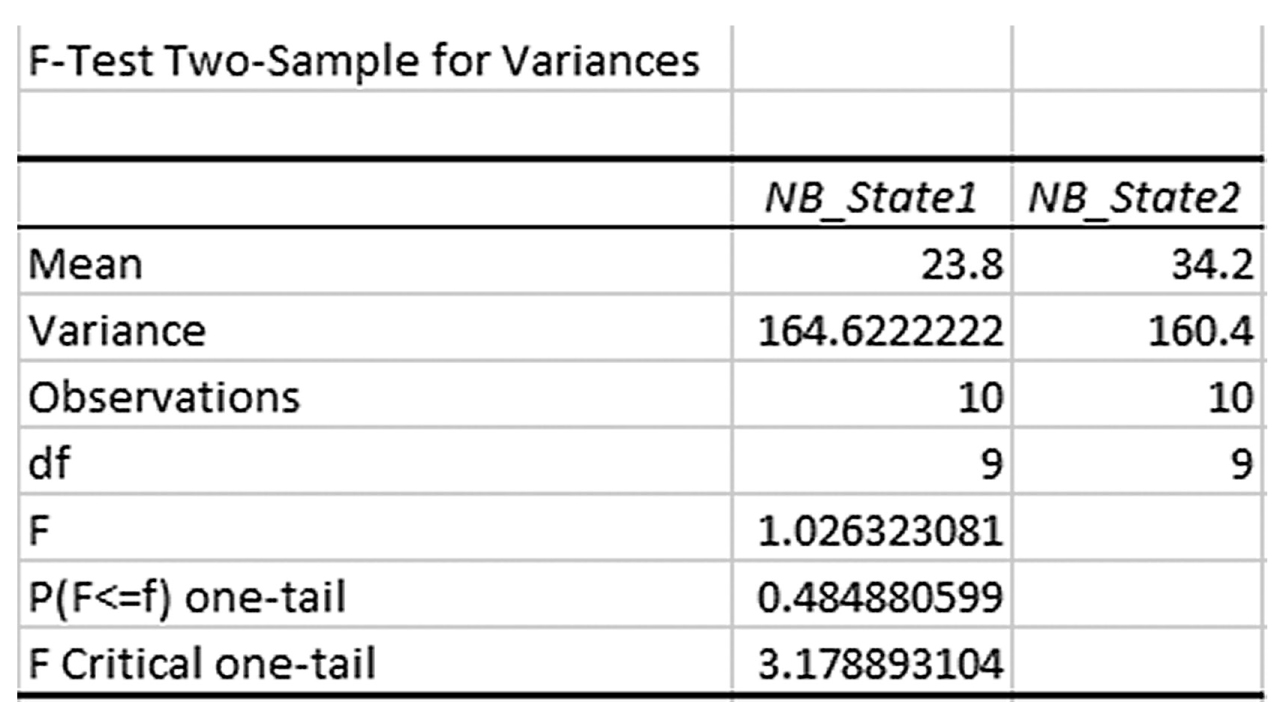
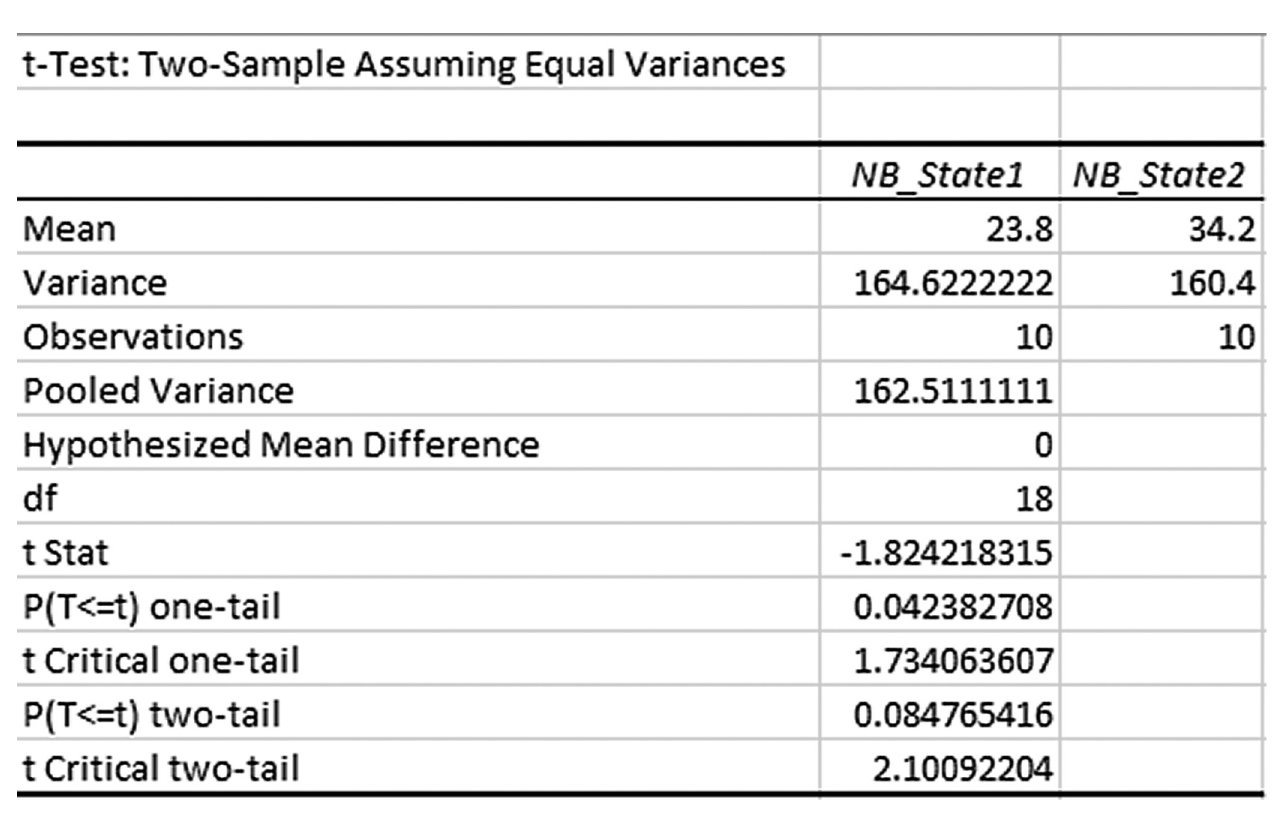
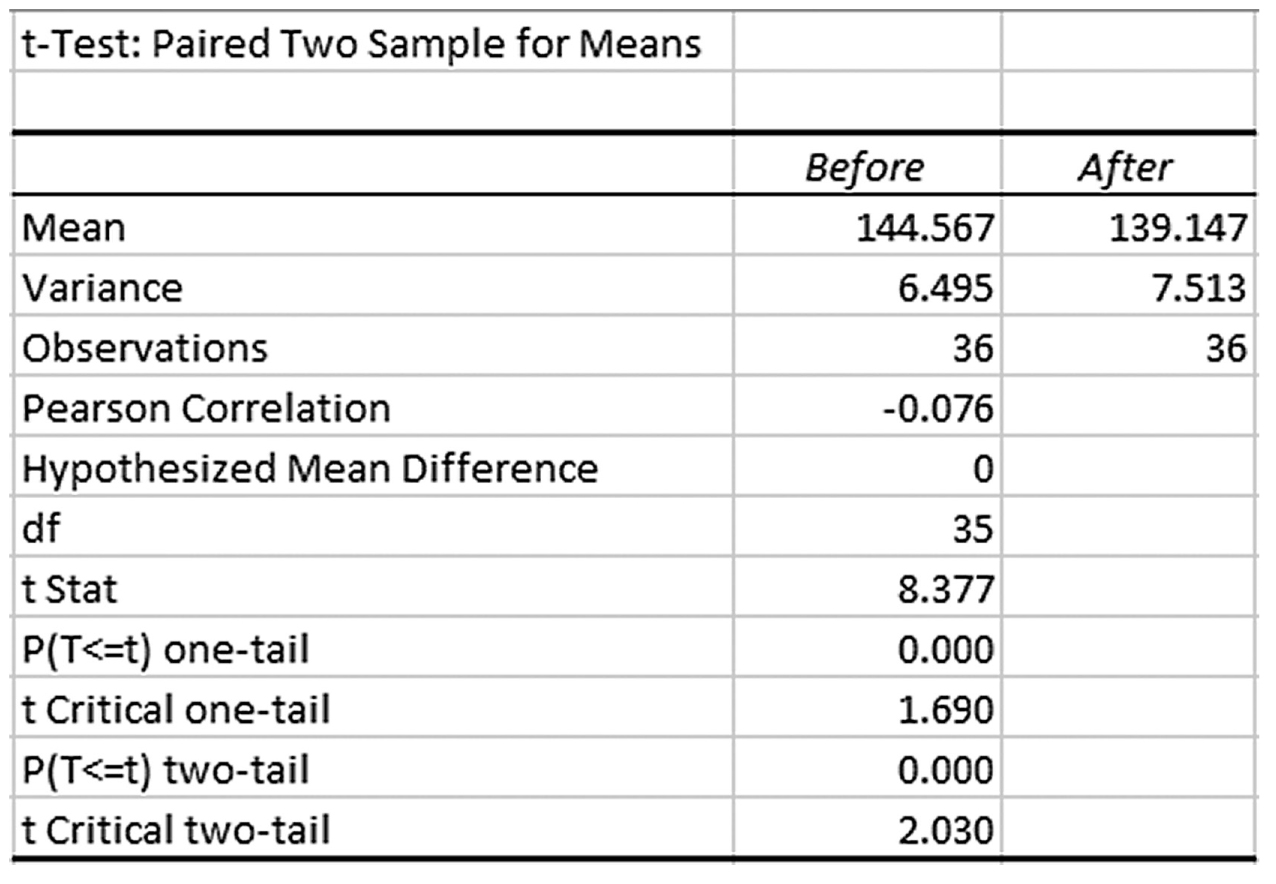
Example output for a one-sample t-test in Excel.

An Excel screenshot displays the output for a one-sample t-test.

Courtesy of Microsoft Excel © Microsoft 2020.

You see that the average IQ of our sample was 123.34 and the t-statistic and corresponding p-value are 2.224 and .028, respectively. A small p-value of .028 indicates that the observed difference between the sample mean and a known population mean of 3.34 units was large enough to rule out chance.

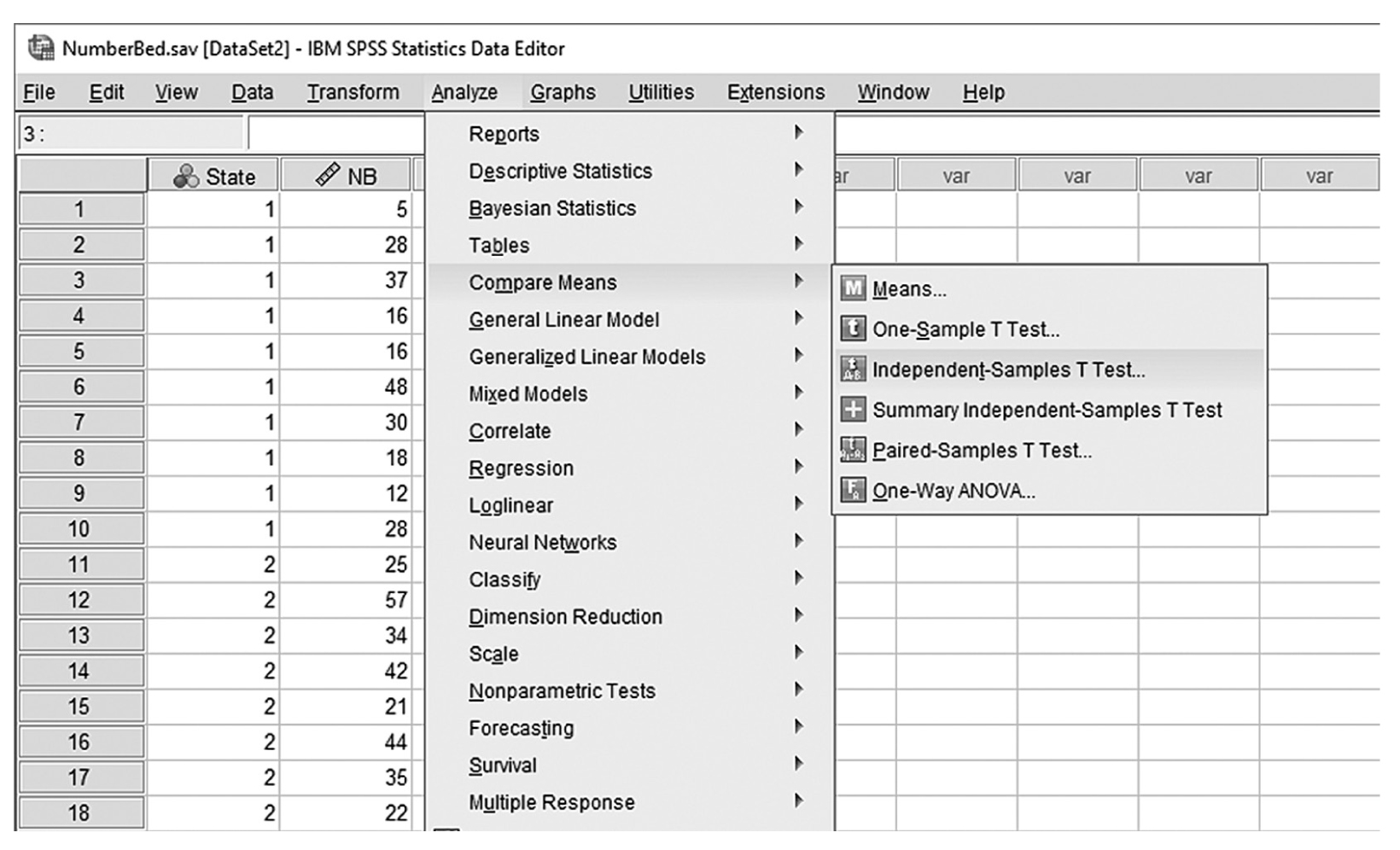
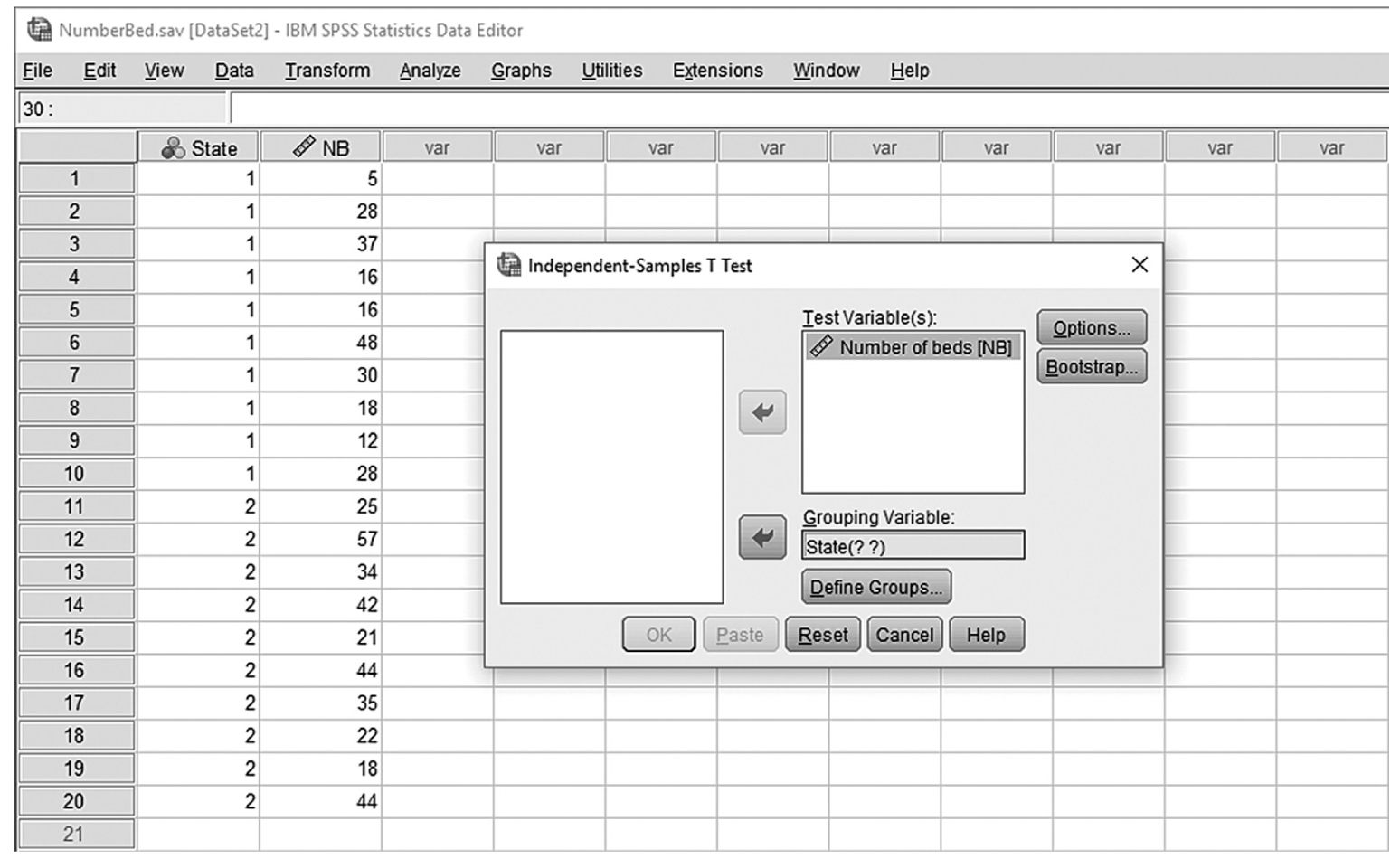
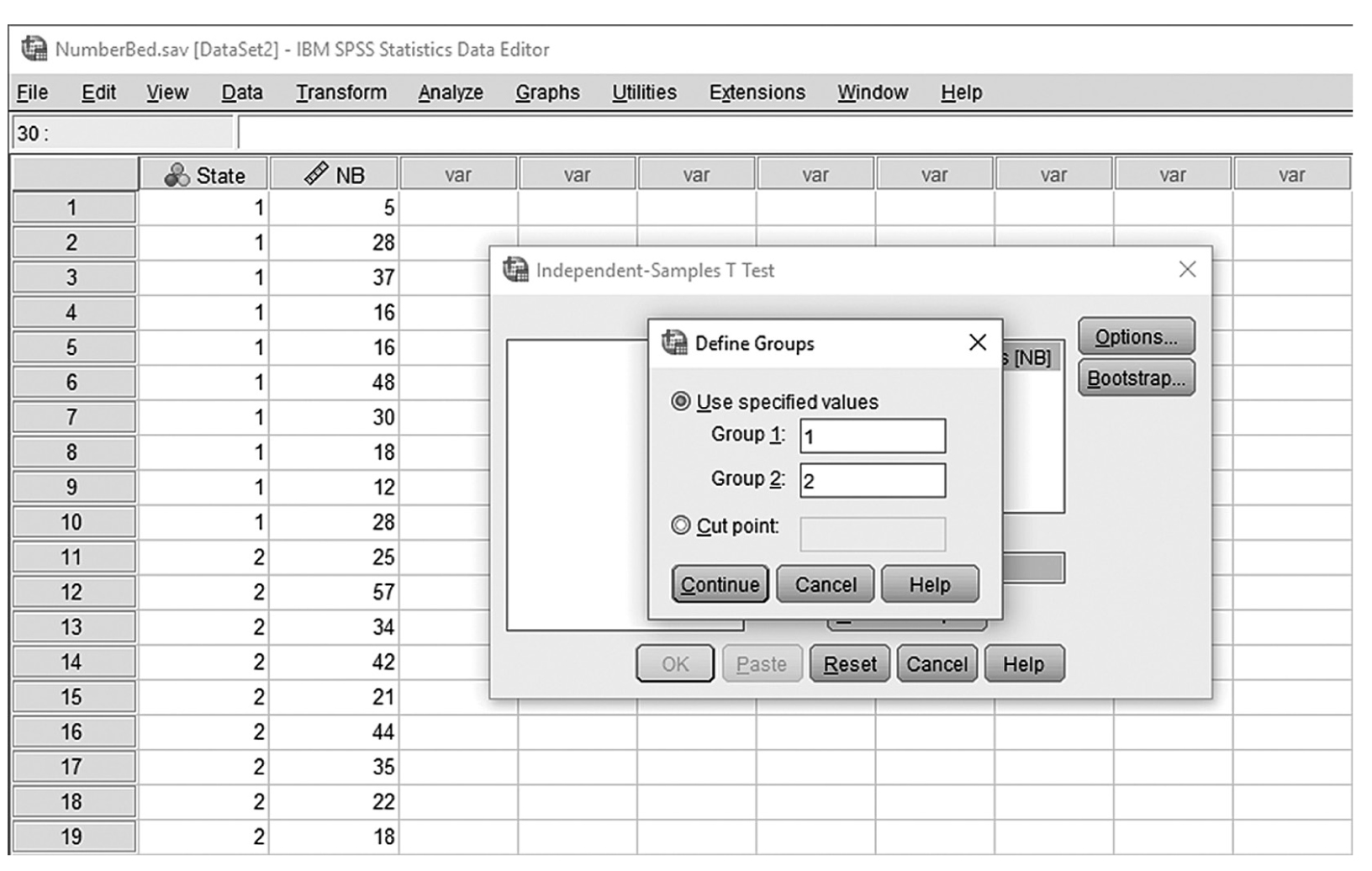
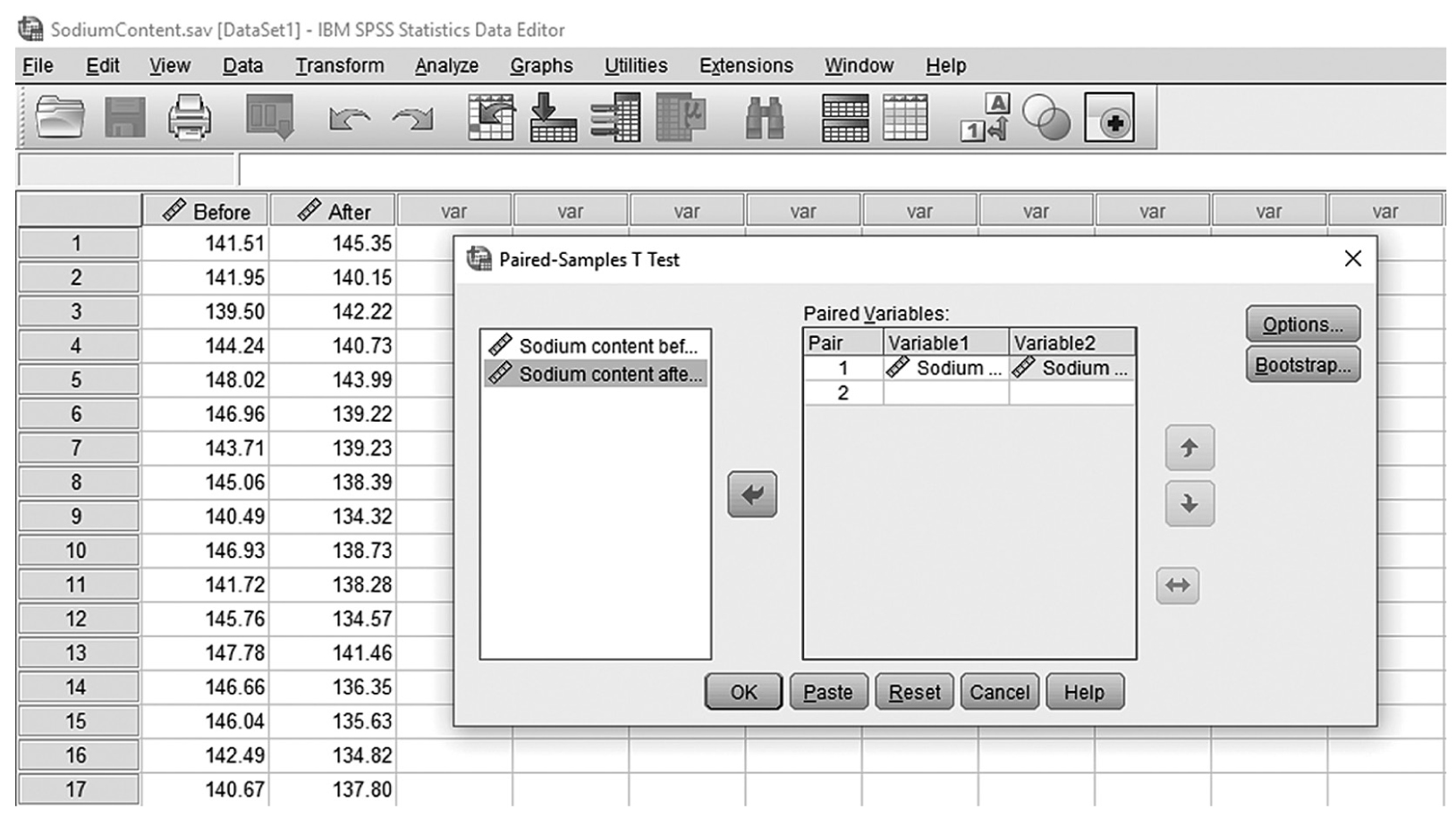
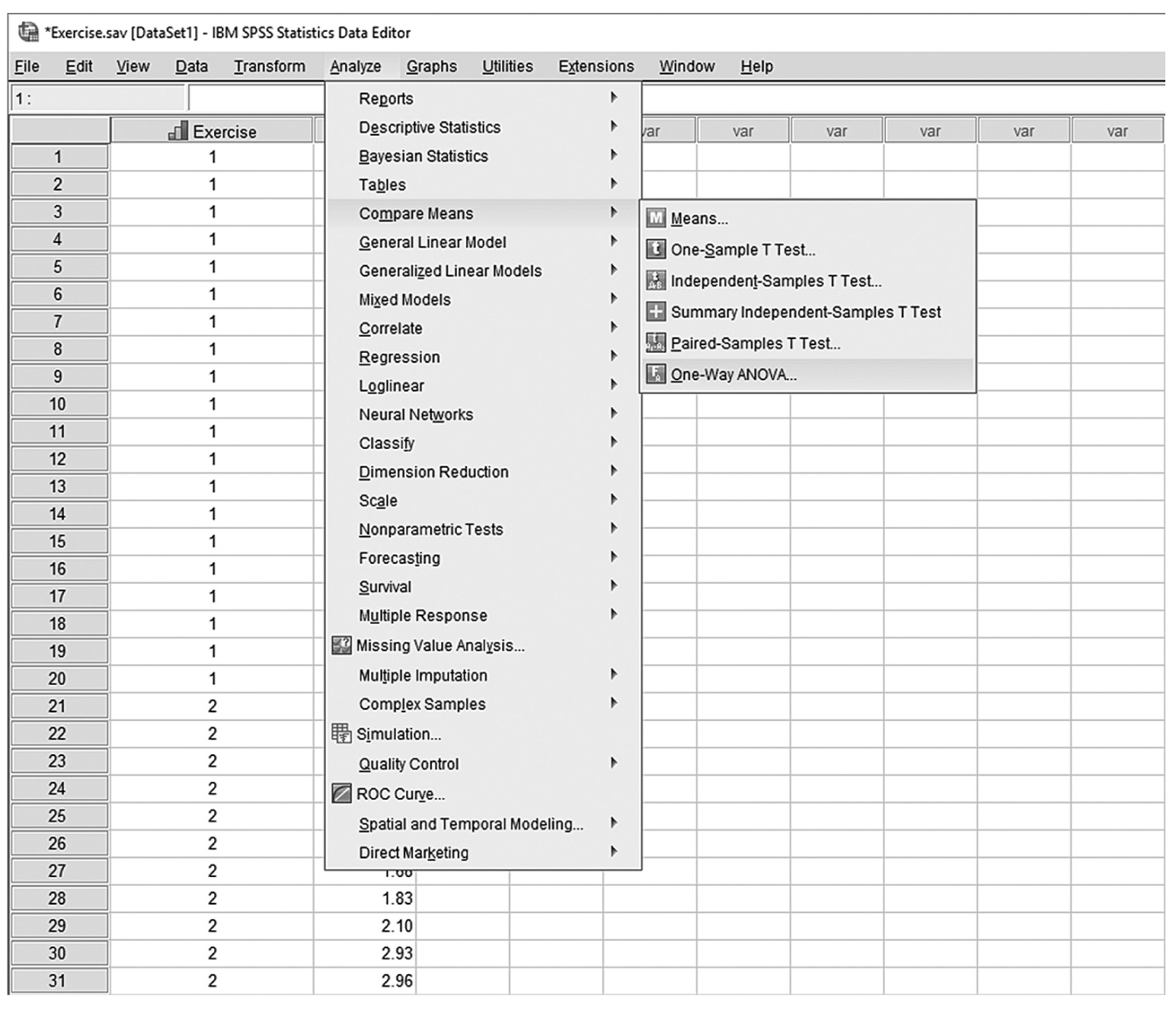
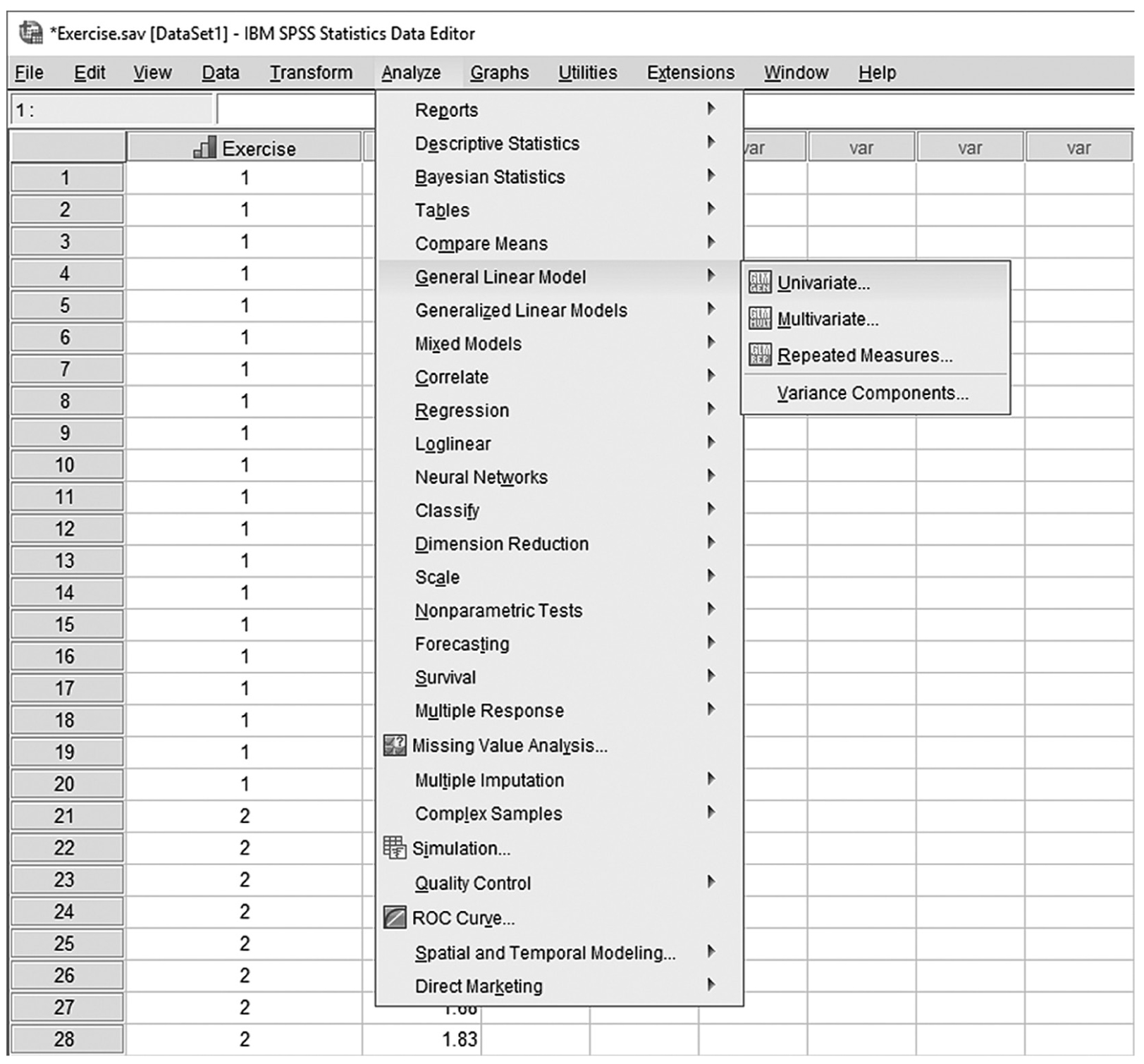
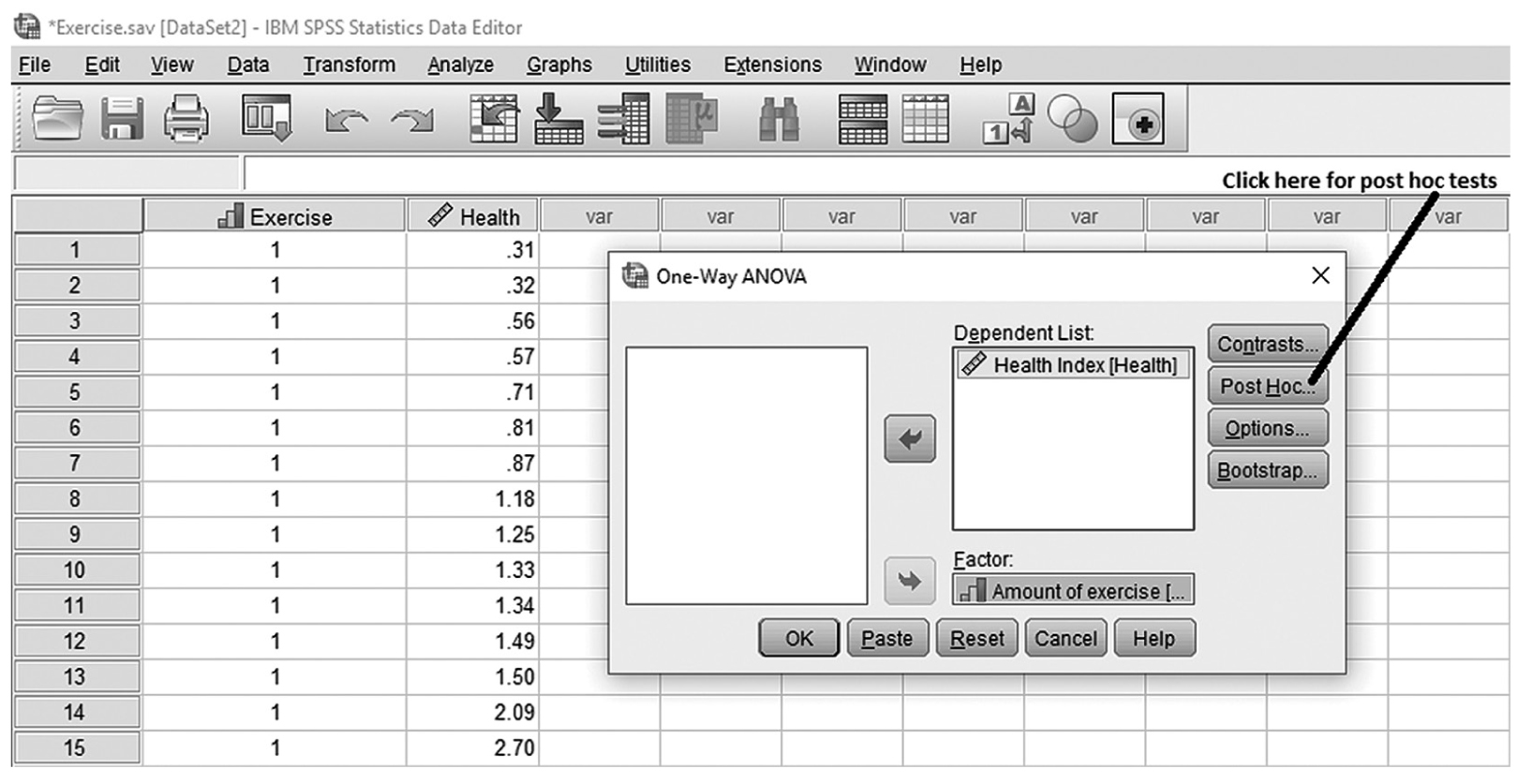
To conduct a one-sample t-test in IBM SPSS Statistics software (SPSS), you will open IQ.sav and go to Analyze > Compare means > One-sample t-test, as shown in Figure 11-6, in this case using IQ measurements from a sample of nursing students. In the One-Sample t-Test dialogue box, you will move IQ into “Test Variable(s)” by clicking on the arrow buttons in the middle and typing in a known population mean (in this case, 120), into “Test Value” (Figure 11-7).

Selecting a one-sample t-test in SPSS.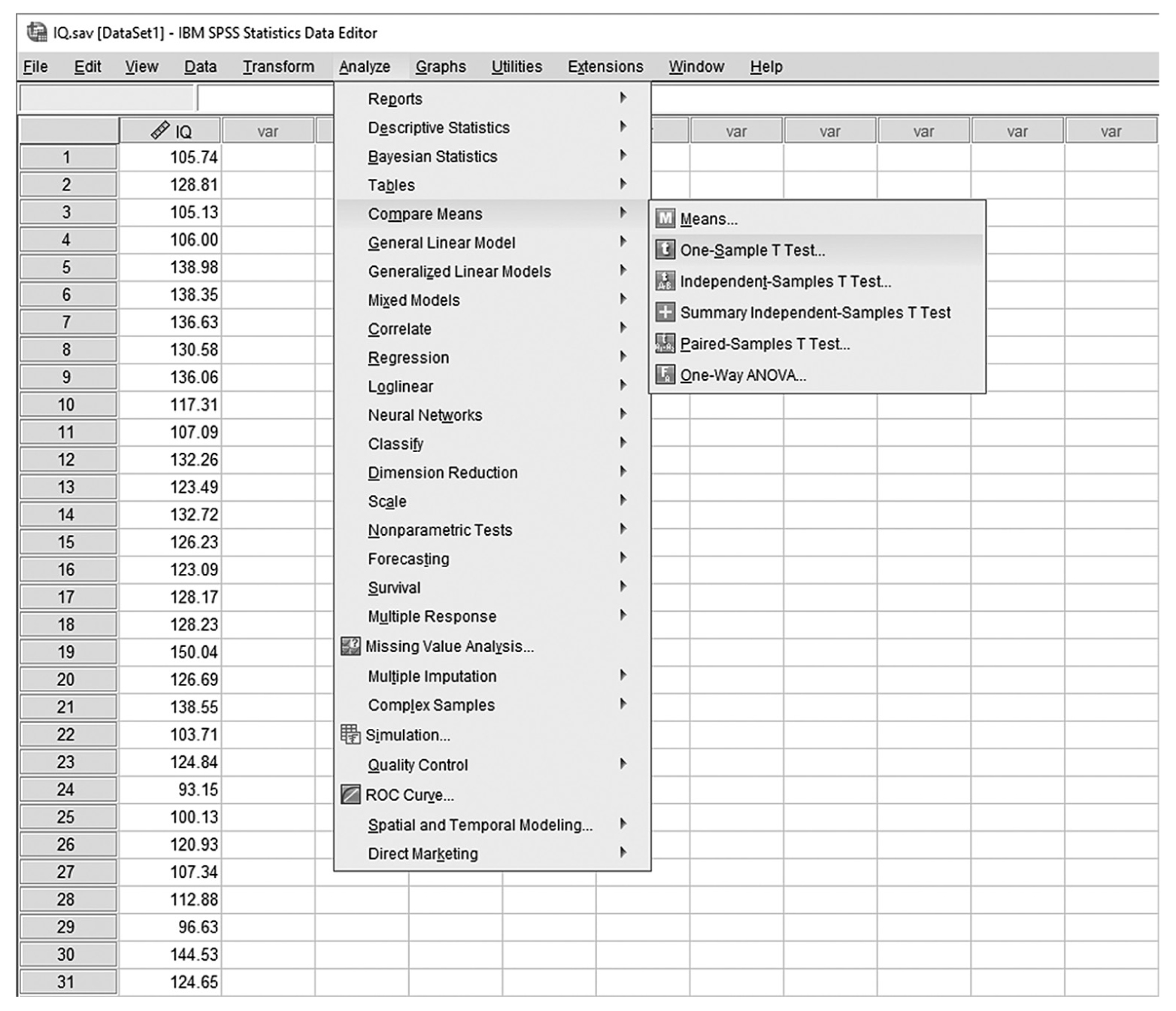

A screenshot in S P S S shows the selection of the Analyze menu, with Compare means command chosen, from which the One-sample t-test option is selected. The data in the worksheet shows a column of numerical data.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation Courtesy of IBM SPSS Statistics.

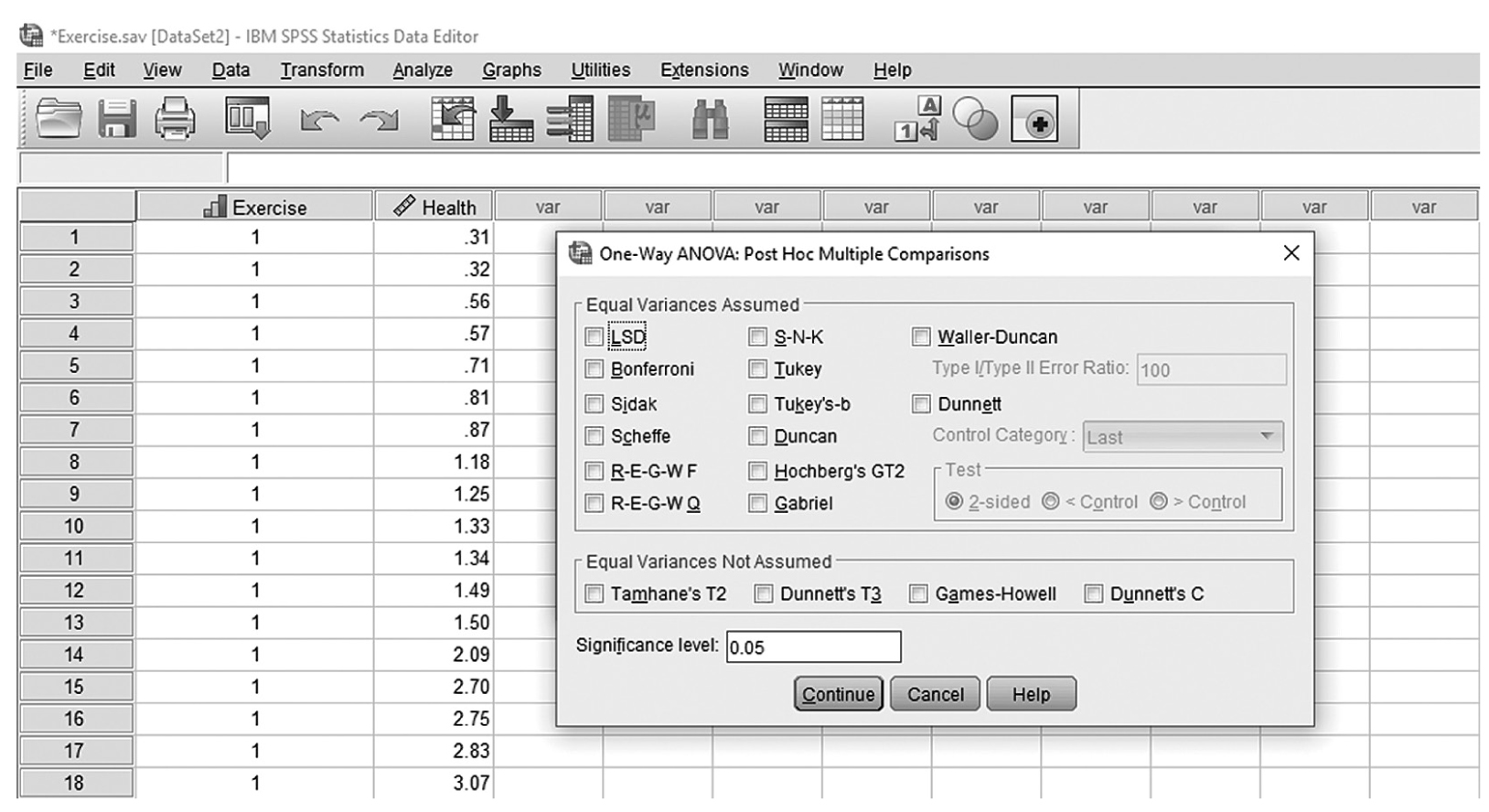
Defining variables in a one-sample t-test in SPSS.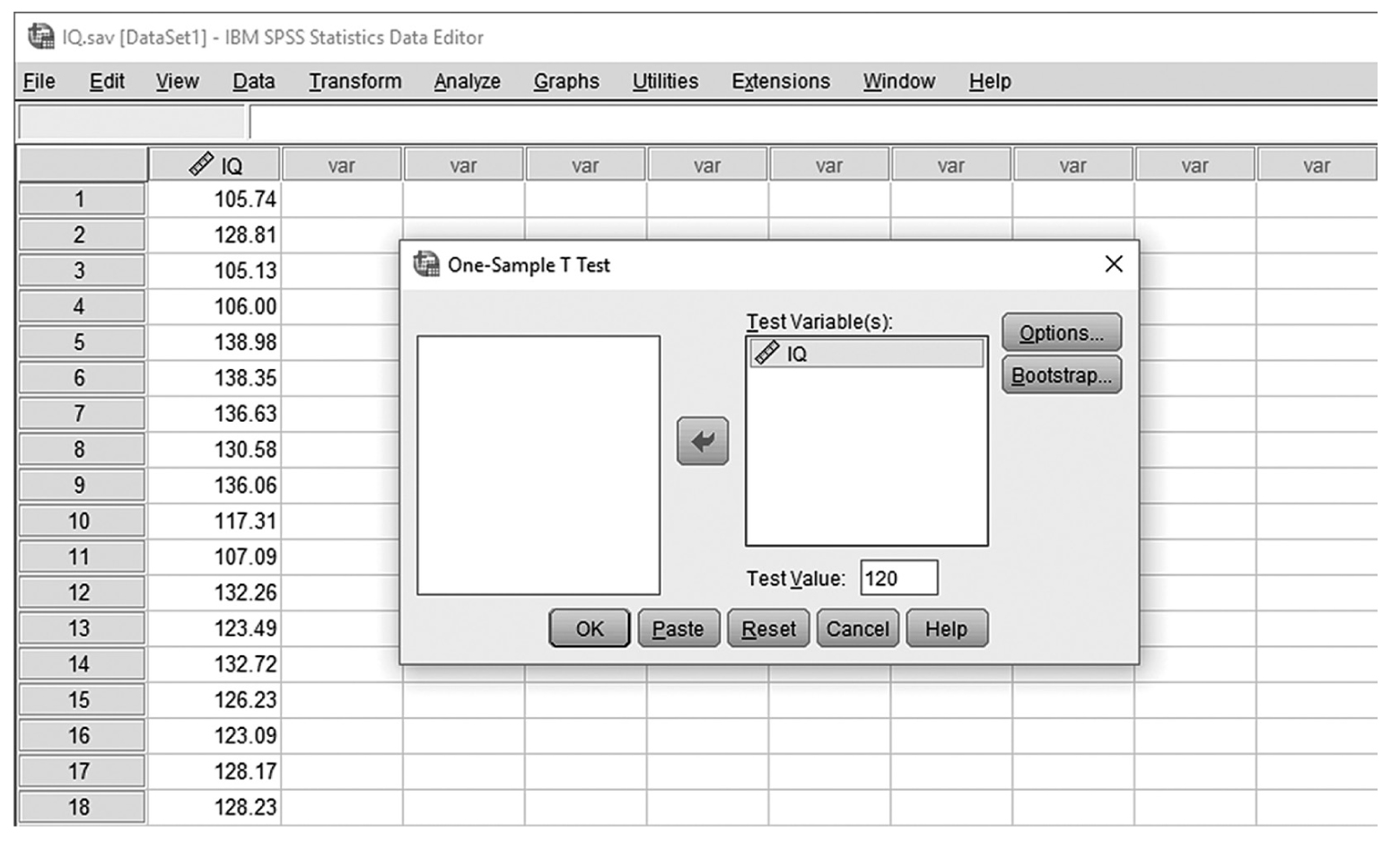

A screenshot in S P S S shows a dialog box with heading, One-sample t-test. Variable I Q is defined in Test variable box. Test value field shows 120. Buttons, Options and Bootstrap, are on right side; Ok, Paste, Reset, Cancel, and Help at the bottom.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

In the Option menu, the confidence interval can be computed based on different confidence levels, and the default is 95%. This menu also gives options for dealing with missing values. The default is to “exclude cases by analysis,” which excludes cases if they have missing values on variables in the current analysis. The other option is to “exclude cases listwise”; this option deletes cases that have any missing values on any variables, whether in the current analysis or a prior one. If cases have even one missing value on a single variable, they will be excluded from the entire analysis, and the analysis is run only on those with complete values. Clicking “OK” will then produce the output of the requested t-test analysis. The example output is shown in Table 11-1.

Table 11-1 Example Output of a One-Sample t-Test

One-Sample Statistics

N

Mean

Std. Deviation

Std. Error Mean

IQ

100

123.3395

15.01559

1.50156

One-Sample Test

Test Value = 120

t

df

Sig. (2-tailed)

Mean Difference

95% Confidence Interval of the Difference

Lower

Upper

IQ

2.224

99

.028

3.33953

0.3601

6.3189

Note that the average IQ was 123.34, the same as that in Excel, with the t-statistic and corresponding p-value of 2.224 and .028, respectively. Again, a small p-value of .028 indicates that the difference of 3.34 units in IQ between the sample and the population was large enough to rule out chance.

Reporting One-Sample t-Test Results

When reporting one-sample t-test results, you should report the size of the t-statistic, the associated p-value, and means and standard error so that readers will know how the sample statistic is different from the known population parameter. Cohen’s d, a type of effect size as discussed in Chapter 7, should also be computed and reported. Results of the t-test for our example for IQ variable could be reported in this way:

  • Nursing students of the current cohort at ABC University had higher IQ scores (M = 123.34, SE = 1.50) than did ABC University students in general, t (99) = 2.22, p = .028, d = .22, 95% CI [0.36, 6.32].

T-Test for Independent Groups ⬆ ⬇

Independent sample t-tests are used when there are two independent groups to be compared on their means. By “independent,” we mean that the subjects in one group cannot also be members of the other group. The t-statistic is computed by dividing the difference between means by an estimate of the standard error of the difference between those two independent sample means. A large deviation between means suggests that the samples from the population differ a lot, and a small deviation between means suggests that samples from the population are more similar.

Rationale

In t-tests, the standard error is used as a gauge of the variability between sample means. When the standard error is large, we will observe large differences in sample means, and we will observe small differences in sample means when the standard error is small. For example, in experimental studies, where we are often comparing treatments or interventions, we reject the null hypothesis when the sample means between the treatment and control groups are substantially different. Otherwise, the difference between sample means is occurring by chance only.

Assumptions

The following parametric assumptions should be met before the independent samples t-test is computed.

  • The sampling distribution should be normal (i.e., the dependent variable should be normally distributed).
  • The data should be measured at the interval level, at least (i.e., continuous measurement).
  • Measurements should be independent (i.e., subjects in these two groups should not overlap).
  • Variances in the groups being compared should be about the same.

Please refer to Chapter 8 for the details about how to check these assumptions.

Doing and Interpreting Independent Samples t-Test

First, we need to set up hypotheses:

H0: There is no difference between group 1 mean and group 2 mean.

Ha: There is a difference between group 1 mean and group 2 mean.

or

H0: μ1 = μ2

Ha: μ1≠μ2.

The test statistic for independent samples t-test can be found by using one of the following formulas:

when sample sizes are equal; or

when sample sizes are not equal

where

If the observed difference between the two means is substantial and the associated p-value is small, we may rule out chance as influencing the difference. When the observed difference is not substantial and the associated p-value is large, that indicates that chance is likely influencing the outcome. As discussed earlier, it is important to support the p-value with a measure of effect size, along with a corresponding interval estimate (i.e., confidence interval) as a measure of importance.

To conduct an independent samples t-test in Excel, you will open NumberBed.xlsx (the data shown in Figure 11-8 are the number of beds in nursing homes in the states of Illinois and Ohio) and go to Data > Data Analysis, as shown in the figure. In the Data Analysis window, you will note that there are “t-Test: Two-Sample Assuming Equal Variances” and “t-Test: Two-Sample Assuming Unequal Variances” on the list (Figure 11-9). So the first thing that you will need to do is to figure out whether variances of the two groups are equal and choose “F-Test Two-Sample for Variances,” as shown in Figure 11-10. This test will check the following hypotheses:

H0: VariANCES OF THE TWO GROUPS ARE EQUAL.

HA: VARIAnces of the two groups are not equal.

or

Finding Data Analysis ToolPak in Excel.

An Excel screenshot shows the Data Analysis ToolPak add-in, in the Analysis group under Data menu.

Courtesy of Microsoft Excel © Microsoft 2020.

Two different independent samples t-tests within the Data Analysis ToolPak in Excel.

An Excel screenshot shows selection of the option, t-Test: Two-Sample Assuming Unequal Variances, within the Data Analysis ToolPak. The worksheet shows two columns, with headings, N B_State 1 and N B_State 2, containing numerical data.

Courtesy of Microsoft Excel © Microsoft 2020.

Selecting “F-Test Two-Sample for Variances” in Excel.

An Excel screenshot shows selection of the option, F-Test Two-Sample for Variances, within the Data Analysis ToolPak. The worksheet shows two columns, with headings, N B_State 1 and N B_State 2, containing numerical data.

Courtesy of Microsoft Excel © Microsoft 2020.

The assumption of equal variance is said to be violated when the p-value is too small to rule out chance and the assumption is said to be not violated otherwise. In the “F-Test Two-Sample for Variances” dialogue box, you will provide A1:A11 as Variable 1 Range, B1:B11 as Variable 2 Range, and D1 as output range with Labels selected (Figure 11-11). Clicking “OK” will then produce the output of requested regression analysis, and the example output is shown in Figure 11-12.

Defining data ranges and selecting options for “F-Test Two-Sample for Variances” in Excel.

An Excel screenshot shows a dialog box with the inputting of data ranges and selecting output options for a one-sample F-test. The worksheet lists N B_State 1 and N B_State 2, with numerical data.

Courtesy of Microsoft Excel © Microsoft 2020.

Example output for “F-Test Two-Sample for Variances” in Excel.

An Excel screenshot displays the output for a one-sample F-test.

Courtesy of Microsoft Excel © Microsoft 2020.

Note that the associated p-value with F statistic is 0.485 so the observed difference between the two variances is not large enough to rule out chance. Therefore, we will select “t-Test: Two-Sample Assuming Equal Variances” in Figure 11-9 and use it in order to test for the difference between the two average number of beds. In the “t-Test: Two-Sample Assuming Equal Variances” dialogue box, you will provide A1:A11 as Variable 1 Range, B1:B11 as Variable 2 Range, “0” for Hypothesized Mean Difference, and D1 as output range with Labels selected (Figure 11-13). Clicking “OK” will then produce the output of requested regression analysis, and the example output is shown in Figure 11-14.

Defining data ranges and selecting options for “t_Test: Two-Sample Assuming Equal Variances” in Excel.

An Excel screenshot shows a dialog box with the inputting of data ranges and selecting output options for a two-sample t-test. The worksheet lists N B_State 1 and N B_State 2, with numerical data.

Courtesy of Microsoft Excel © Microsoft 2020.

Example output for “t_Test: Two-Sample Assuming Equal Variances” in Excel.

An Excel screenshot displays the output for a two-sample t-test.

Courtesy of Microsoft Excel © Microsoft 2020.

To conduct an independent samples t-test in SPSS, you will open NumberBed.sav and go to Analyze > Compare means > Independent samples t-test, as shown in Figure 11-15. In the Independent Samples t-Test dialogue box, you will move a dependent variable, “NB,” into “Test Variable(s)” and the independent variable, “State,” into “Grouping Variable” by clicking the corresponding arrow buttons in the middle, as seen in Figure 11-16. You will notice that the “OK” button is not active because we have not defined our two groups. As you see in Figure 11-17, we have defined the coding of 1 for Illinois and 2 for Ohio. Click on the “Define Groups” button and assign 1 for group 1 (Illinois) and 2 for group 2 (Ohio) (Figure 11-18). Clicking “Continue” and then “OK” will produce the output of the requested analysis. The example output is shown in Table 11-2.

Selecting an independent samples t-test in SPSS.

A screenshot of an S P S S Editor shows the selection of the option, Independent samples t-test, from the drop-down list of Compare Means under the Analyze menu. There are two columns, State and N B, with rows of numerical data under each column.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

Defining variables in an independent samples t-test in SPSS.

A screenshot in an S P S S shows a dialog box, where variables are defined in an independent samples t-test. There are two columns, State and N B, with rows of numerical data under each column.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

Coding scheme for “State” variable.

A screenshot in S P S S depicts the coding scheme for the variable, State.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

Defining groups in an independent samples t-test in SPSS.

A screenshot in S P S S shows a dialog box, where groups are defined in an independent samples t-test. There are two columns, State and N B, with rows of numerical data under each column.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

Table 11-2 Example Output of an Independent Samples t-Test in SPSS

Group Statistics

State

N

Mean

Std. Deviation

Std. Error Mean

Number of beds in ­nursing homes

IL

10

23.80

12.831

4.057

OH

10

34.20

12.665

4.006

Independent Samples Test

Levene’s Testfor Equality of Variances

t-Test for Equality of Means

F

Sig.

t

df

Sig. (2-tailed)

Mean Difference

Std. Error Difference

95% Confidence Interval of the Difference

Lower

Upper

Number of beds in ­nursing homes

Equal variances assumed

.004

.947

-1.824

18

.085

-10.400

5.701

-22.378

1.578

Equal variances not assumed

-1.824

17.997

.085

-10.400

5.701

-22.378

1.578

Notice that the average number of nursing home beds per nursing home in the state of Illinois is 23.8, and in the state of Ohio, the average is 34.2. We see that there is, on average, about a 10-bed difference between the two states; the question is whether this difference of 10 beds is substantial. Recall one of the assumptions was that the variability of the two groups is about the same. Independent samples t-test outputs in SPSS include the results of Levene’s test, which checks this assumption.

The assumption of equal variance is said to be violated when the p-value is too small to rule out chance and the assumption is said not to be violated otherwise. You should interpret the results of an independent samples t-test according to this result. If the equal variance assumption is met, you should interpret the first row of the output, “Equal variances assumed,” and the second row of the output, “Equal variances not assumed,” if the equal variance assumption is not met. In our example, the assumption of equal variances is not violated, so we will interpret the “Equal variances assumed” row of the output. The computed t-statistic and corresponding p-value are μ1.824 and .085, respectively. Because the p-value is large, the null hypothesis is not rejected, and it is determined that the average number of beds in Illinois and Ohio nursing homes is said to be roughly the same.

Reporting Independent Samples t-Test Results

When reporting independent samples t-test results, you should report the size of the t-statistic and associated p-value and also report means and standard error so that the readers will know how the two sample means differ. Another type of effect size, r, as discussed in Chapter 7, can be computed with the following equation:

and reported for the independent sample t-test. The following is a sample report for this example:

On average, the number of beds in Illinois nursing homes (M = 23.8, SE = 4.06) was not different from the number of beds in Ohio nursing homes (M = 34.2, SE = 4.01), t(18) = μ1.83, p = .085, r = .40, 95% CI [μ22.38, 1.58].

T-Test for Dependent Groups ⬆ ⬇

We use the dependent sample t-test when the measurements of a given dependent variable are paired. By dependent samples, we mean that we are dealing with a single group of participants; therefore, their responses to one set of measurements are related to another. There are two ways that measurements can be paired. First, one sample can be measured twice, such as when the systolic blood pressure (SBP) of a group of patients was measured before and after they received an antihypertensive drug. Second, two different data sets can be paired, such as in the Kurnat-Thoma, Edwards, and Emery (2018) case study, when a group of participants had their body temperature measured with two different non-invasive devices. The statistic is computed in the same way as in the independent samples t-test, in that the difference between the means is divided by some form of the standard error. Measurements will differ a lot if there is a large deviation between means, and measurements will not differ much if there is small deviation between means. The same rationale discussed previously for the independent samples t-test still applies for the dependent samples t-test.

Assumptions

As measurements will not be independent, we cannot assume that the last two assumptions of the independent t-test, which are the assumptions of equal variance and independent measurements, are valid. However, the normality of sampling distribution and data being measured at the interval level still apply.

One thing to note about the two assumptions for a dependent samples t-test is that what has to be measured at least at the interval level and to be normally distributed are not the measurements themselves. It is, in fact, the difference between the two sets of measurements that must be measured at the interval level and normally distributed. For example, we need to check the level of measurement and normality of the difference between systolic blood pressure measurements before and after receiving an antihypertensive drug, not the before and after measurements themselves. Therefore, the first task is to calculate the difference between the measurements for each case in the data set, and then you should examine the level of measurements and the normality of it.

Doing and Interpreting the Dependent Samples t-Test

First, we need to set up hypotheses:

H0: There is no difference between before measurements and after measurements.

Ha: There is a difference between before measurements and after measurements.

or

The test statistic for dependent samples t-test can be found by the following equation:

where

D

is the mean difference between sample measurements, μD is the hypothesized mean difference between population measurements, SD is the standard error of the difference, and n is the sample size. Once the statistic is computed, the associated p-value can be reported as a quantified measure against the null, but it is again left to the researcher with substantive knowledge to decide whether the difference between the means is meaningful.

To conduct a dependent samples t-test in Excel, you will open SodiumContent.xlsx and go to Data > Data Analysis, as shown in Figure 11-19. In the Data Analysis window, choose “t-Test: Paired Two Sample for Means” in the list and then click “OK” (Figure 11-20). In the Linear “t-Test: Paired Two Sample for Means” dialogue box, you will provide A1:A11 as Variable 1 Range, B1:B11 as Variable 2 Range, “0” for Hypothesized Mean Difference, and D1 as output range with Labels selected (Figure 11-21). Clicking “OK” will then produce the output of requested regression analysis, and the example output is shown in Figure 11-22.

Finding Data Analysis ToolPak in Excel.

An Excel screenshot shows the Data Analysis ToolPak add-in, in the Analysis group under Data menu.

Courtesy of Microsoft Excel © Microsoft 2020.

Selecting “t-Test: Paired Two Sample for Means” in Excel.

An Excel screenshot shows selection of the option, t-Test: Paired Two Sample for Means, within the Data Analysis ToolPak. The worksheet shows two columns, with headings, Before and After, containing numerical data.

Courtesy of Microsoft Excel © Microsoft 2020.

Defining data ranges and selecting options for “t-Test: Paired Two Sample for Means” in Excel.

An Excel screenshot shows a dialog box with the inputting of data ranges and selecting output options for a two-sample t-test. The worksheet lists Before and After, with numerical data.

Courtesy of Microsoft Excel © Microsoft 2020.

Example output for “t-Test: Paired Two Sample for Means” in Excel.

An Excel screenshot displays the output of requested regression analysis.

Courtesy of Microsoft Excel © Microsoft 2020.

To conduct a dependent samples t-test in SPSS, you will open SodiumContent.sav and go to Analyze > Compare means > Paired samples t-test, as shown in Figure 11-23. The data shown in this figure are the sodium content levels in a sample of patients both before and after a new diet. In the Paired Samples t-Test dialogue box, then you will move the variables to be paired into “Paired Variables,” in order, by clicking the corresponding arrow buttons in the middle, as shown in Figure 11-24. Clicking “OK” will then produce the output of the requested analysis. An example output is shown in Table 11-3.

Selecting a dependent samples t-test in SPSS.

A screenshot of an S P S S Editor shows the selection of the option, Paired samples t-test, from the drop-down list of Compare Means under the Analyze menu. There are two columns, Before and After, with rows of numerical data under each column.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

Defining variables in a dependent samples t-test in SPSS.

A screenshot in S P S S shows a dialog box, where variables are defined in a dependent samples t-test. The worksheet shows two columns, with headings, Before and After, containing numerical data.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

Table 11-3 Example Output of a Dependent Samples t-Test in SPSS

Paired Samples Statistics

Mean

N

Std. Deviation

Std. Error Mean

Pair 1

Sodium content before a new diet

144.5666

36

2.54909

0.42485

Sodium content after 2 weeks on a new diet

139.1459

36

2.74068

0.45678

Paired Samples Correlations

N

Correlation

Sig.

Pair 1

Sodium content before a new diet and sodium content after 2 weeks on a new diet

36

-0.076

.658

Paired Samples Test

Paired Differences

95% Confidence Interval of the Difference

Mean

Std. Deviation

Std. Error Mean

Lower

Upper

t

df

Sig. (2-tailed)

Pair 1

Sodium content before a new diet and sodium content after 2 weeks on a new diet

5.42061

3.88285

.64714

4.10684

6.73438

8.376

35

.000

Observe that the average sodium content level before the new diet is 144.6 units, and the average sodium content level after a new diet is 139.1 units. We see a difference of 5.4 units in sodium content level between the before and after measurements. The question now is whether this difference of 5.4 units of sodium is meaningful. The second section in Table 11-3 shows that the measurements are not substantially correlated, with a correlation coefficient of μ.08 and its associated p-value of .658. The computed t-statistic and corresponding p-value are 8.376 and .000, respectively. Because the p-value of .000 is very small, we reject the null hypothesis, having determined that the average sodium content level before the new diet is substantially higher than the one measured after the new diet.

Reporting Dependent Samples t-Test

When reporting dependent samples t-test results, you should report the size of the t-statistic, associated p-value, and the means and standard error so that readers will know how the before and after sample means are different from each other. Similar to the independent samples t-test, r can be computed and reported for the dependent sample t-test. The following is a sample report from our example:

On average, the sodium content level after the new diet (M = 144.6, SE = 0.42) was substantially lower than that before the new diet (M = 139.1, SE = 0.46), t (35) = 8.38, p = .000, r = .82, 95% CI [4.11, 6.73].

One-Way Analysis of Variance ⬆ ⬇

The independent t-test allows us to compare the means of two independent groups and to make decisions on whether these are different. But what if we have more than two groups to compare? For example, a nurse investigator is interested in testing the effectiveness of a newly developed diet using three groups: a placebo group, an existing diet group, and a new diet group. Because the independent t-test is only designed to test two group means, the simultaneous comparison of these three groups is not possible. You may be thinking that it is possible to conduct three independent samples t-tests by comparing the following pairs: placeboμexisting diet, placeboμnew diet, and existing dietμnew diet. However, there is an increased risk of Type I error if we conduct multiple tests this way, and this increased risk gets worse as the number of tests increases (i.e., the actual risk of Type I error will increase as the number of tests increases). This will be true for any set of statistical tests.

For any given set of statistical tests, the inflated Type I error will be:

where αinflated is the inflated Type I error after conducting multiple tests, αprespecified is the prespecified/desired Type I error, and n is the number of tests. As you can see, the risk of Type I error will be inflated as more tests are conducted. For example, if you run three tests, each at a Type I error of .05, the Type I error is inflated to

and running five tests will inflate the Type I error to

So, what do .1426 and .2262 mean? They mean that you have a higher probability of committing a Type I error by conducting multiple tests (i.e., you will be more likely to falsely reject the true null hypothesis). Therefore, you should control for an inflated Type I error somehow, so that you will not incorrectly reject the true null hypothesis more frequently than you desired.

A better statistical test to identify three or more group differences is analysis of variance (ANOVA), which compares all groups simultaneously and so captures the overall differences across groups. However, ANOVA only tells us that there exists a group difference; it does not tell us specifically which groups differ. We offer an example of this in the next section.

Assumptions

All assumptions of an independent samples t-test also apply to one-way ANOVA, as it is a natural extension of an independent samples t-test. These parametric assumptions are as follows:

  • The sampling distribution should be normal (i.e., the dependent variable should be normally distributed).
  • The dependent variable data should be measured at least on an interval level (i.e., continuous measurement).
  • Variances in the groups in the comparison should be about the same.
  • The measurements should be independent (i.e., subjects in the groups should not overlap).

Please refer again to Chapter 8 for details about how to check these assumptions.

Doing and Interpreting One-Way ANOVA

First, we need to set up hypotheses:

H0: There is no difference among group means.

Ha: At least two group means differ.

or

H0: μ1 = μ2 = μ3

Ha: μj≠μk for some j and k

Again, the alternative hypothesis cannot be written as

Ha: μj≠μk for all j and k

because we do not know if all groups differ or if just two or three groups differ. The test statistic for one-way analysis of variance can be found by the following equation:

where both differences are shown in Figure 11-25. The small p-value such as .000 would lead us to reject the null hypothesis, saying that the groups do not differ because it would indicate that we would observe the difference as extreme as our statistic in almost 0 sample out of 1,000, and we will not reject the null hypothesis otherwise. From the figure, it is clear that the differences between groups will be more likely to be present as the difference between groups gets larger (i.e., the statistic will likely fall in the rejection region as it gets larger).

Visual representation of between- and within-group differences.

An illustration depicts between-group differences and within-group differences, where each group is represented as a bell-shaped curve.

The within-groups difference can be thought of as individual differences and is the variability in the data not explained by variables in the study (i.e., error). The between-groups difference can be easily shown in the data in terms of means; this is the variability in the data that is explained by the variables in the study. When the variability explained by the variables under study is larger than that not explained by the variables under study, the results indicate that there is a difference among groups. Note that a large within-group difference is not desirable because it is more difficult to find the between-group difference when the individuals within groups are very dissimilar. In other words, the results may not pick up a group difference, even with substantial difference between means, if individuals within groups differ greatly. Refer to Figure 11-26 for an understanding of how the groups differ in the scenario on the left (less within-group difference) from the one on the right (more within-group difference).

Undesirable effect of within-group differences in ANOVA.

Two illustrations depict the two outcomes of varying within-group differences.

To conduct a one-way ANOVA in Excel, you will open Exercise.sav and go to Data > Data Analysis, as shown in Figure 11-27. In the Data Analysis window, choose “ANOVA: Single Factor” and then click “OK” (Figure 11-28). In the “ANOVA: Single Factor” dialogue box, you will provide A1:D21 as Input Range and F1 as Output Range with Labels in First Row selected (Figure 11-29). Clicking “OK” will then produce the output of requested ANOVA. The example output is shown in Figure 11-30.

Finding Data Analysis TookPak in Excel.

An Excel screenshot shows the Data Analysis ToolPak add-in, in the Analysis group under Data menu.

Courtesy of Microsoft Excel © Microsoft 2020.

Selecting “ANOVA: Single Factor” in Data Analysis Window in Excel.

An Excel screenshot shows selection of option, ANOVA: Single Factor, in the Data Analysis dialog box. The worksheet has four columns, No Exercise, 1 day per week, 3 day per week, and 5 day per week, with corresponding rows of data under each column.

Courtesy of Microsoft Excel © Microsoft 2020.

Defining input range and output range in “ANOVA: Single Factor” in Excel.

An Excel screenshot shows the ANOVA: Single Factor dialog box with fields to define data. The worksheet has four columns, No Exercise, 1 day per week, 3 day per week, and 5 day per week, with corresponding rows of data under each column.

Courtesy of Microsoft Excel © Microsoft 2020.

Example output of ANOVA: Single Factor in Excel.

An Excel screenshot displays the output of ANOVA: Single Factor. There are two tables.

Courtesy of Microsoft Excel © Microsoft 2020.

To conduct a one-way ANOVA in SPSS, you will open Exercise.sav and can go to either Analyze > Compare means > One-way ANOVA or Analyze > Generalized linear models > Univariate, as shown in Figure 11-31 and Figure 11-32, respectively. The data shown in the figures represent the amount of exercise as an independent variable and health index as a dependent variable. We will first examine how to conduct one-way ANOVA in Analyze > Compare means > One-way ANOVA. In the One-Way ANOVA dialogue box, you will move an independent variable into “Factor” and a dependent variable into “Dependent List” by clicking the corresponding arrow buttons in the middle (see Figure 11-33). There are three buttons in the box; click on the “Options” button for now and check “Descriptives” and “Homogeneity of variance test” (see Figure 11-34). Clicking “Continue” and then “OK” will then produce the output of requested ANOVA analysis. Example output is shown in Table 11-4.

Selecting one-way ANOVA under “Compare Means” in SPSS.

A screenshot in S P S S shows the selection of the Analyze menu, with Compare means command chosen, from which the one-way ANOVA option is selected. The data in the worksheet shows columns of numerical data.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

Selecting one-way ANOVA under “General Linear Models” in SPSS.

A screenshot in S P S S shows the selection of the Analyze menu, with Generalized linear models command chosen, from which the one-way ANOVA option is selected. The data in the worksheet shows columns of numerical data.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

Defining variables in one-way ANOVA in SPSS.

A screenshot in S P S S Editor defines variables in one-way ANOVA. The numerical data in the worksheet lists Exercise and Health values.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

Selecting options in one-way ANOVA in SPSS.

A screenshot shows the selection of options in one-way ANOVA in a dialog box in an Excel worksheet.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

Table 11-4 Example Output of One-Way ANOVA in SPSS

Descriptives

Health Index

95% Confidence Interval for Mean

N

Mean

Std. Deviation

Std. Error

Lower Bound

Upper Bound

Minimum

Maximum

None

20

1.6031

1.05270

.23539

1.1104

2.0958

.31

4.11

1 day per week

20

4.1101

4.4091

.98609

2.0462

6.1740

.40

18.21

3 days per week

20

4.7725

5.00301

1.11871

2.4310

7.1140

.33

18.47

5 days per week

20

5.4866

6.03848

1.35025

2.6605

8.3127

.35

21.08

Total

80

3.9931

4.67988

.52323

2.9516

5.0345

.31

21.08

Test of Homogeneity of Variances

Health Index

Levene Statistic

df1

df2

Sig.

5.799

3

76

.001

ANOVA

Health Index

Sum of Squares

df

Mean Square

F

Sig.

Between groups

171.276

3

57.092

2.783

0.047

Within groups

1558.928

76

20.512

Total

1730.203

79

You will see that the health problem index for the “no exercise” group is 1.60, which seems to be lower than the index of the other three groups. The group that exercised once a week showed a health index of 4.11, the group that exercised 3 days per week had a health index of 4.77, and the group that exercised 5 days per week showed a health index of 5.49. So, is the difference among these four groups substantial enough to say that it is an effect of exercise?

Levene’s test results for the homogeneity of variance assumption indicate that this assumption is violated. Recall that this test assumes the variances across the groups be equal, so a small p-value of .001, as shown in Table 11-4, leads us to reject the null hypothesis concluding that the variances are not the same. One thing to note here is that when the sample sizes across all groups are the same, one-way ANOVA is known to be robust to the violation of equal variances as well as that of normality. Therefore, we can somewhat ignore this violation.

The ANOVA table shows the F-statistic (this is the statistical test reflecting the F-distribution used in all ANOVAs) and the associated p-values of 2.783 and .047, respectively. Because the p-value of .047 is small enough to rule out chance, the null hypothesis is rejected and the health index is different between/among at least two exercise groups.

Reporting One-Way ANOVA

When reporting one-way ANOVA results, you should report the size of the F-statistic along with the associated degrees of freedom and associated p-value. The effect size for one-way ANOVA results is called omega squared (ω2) and is found with the following equation:

where SSR is the sums of squares for regression, dfR is the degrees of freedom for regression, MSE is the mean squares for residual, and SST is the total sums of squares. Note that ω2 can only be calculated when the group sample sizes are equal.

The following is a sample report of our example.

There was a weak effect of the amount of exercise per week on health index, F (3, 76) = 2.78, p = .047, ω2 = .06.

Multiple Comparisons ⬆ ⬇

If we had concluded that the amount of exercise did not make a difference on the health index and we decided not to reject the null hypothesis, then no further analysis would be needed. In our previous example, however, further analysis is needed because the amount of exercise made a substantial difference on the health index. Remember that a one-way ANOVA result with a small p-value does not necessarily tell us which of the groups differ. Therefore, we need to conduct further comparisons to find out exactly how the groups differ from each other; these analyses are called planned contrasts and post hoc tests.

Doing and Interpreting Multiple Comparisons

Orthogonal planned contrasts, sometimes called a priori tests, are used when specific comparisons are determined before an examination of the data because you expect specific means to differ. These comparisons are often theory driven and protect us from overly increasing Type I error. To set orthogonal planned contrasts, there are some rules to follow when choosing the theory-driven comparisons:

  • Rule #1: Groups that are included in the comparison get either positive or negative weights. Groups that have positive weights are compared with groups that have negative weights.
  • Rule #2: Groups that are excluded from the comparison get zero weights.
  • Rule #3: The sum of all weights in the comparison adds up to zero.

Recall that we found that the effect of the amount of exercise differed in our previous example, and we are specifically interested in whether exercising more than 3 days a week improves the health index. We then apply positive weights of +1 to 3 days per week and 5 days per week and negative weights of μ1 to none and 1 day per week. These weights create orthogonal planned contrasts, as they sum up to zero.

Consider next that we are interested in whether exercising even 1 day per week improves the health index. We then apply a positive weight of +3 to none and negative weights of μ1 to 1 day per week, 3 days per week, and 5 days per week. These weights sum up to zero, so they are orthogonal planned contrasts. These examples of contrast weights are summarized in Table 11-5.

Table 11-5 Example of Contrast Weights

None

1 Day per Week

3 Days per Week

5 Days per Week

Example 1

-1

-1

+1

+1

Example 2

+3

-1

-1

-1

To conduct planned contrasts in SPSS, click on the “Contrasts” button in the One-Way ANOVA dialogue box, as shown in Figure 11-35; the One-Way ANOVA Contrasts dialogue box is shown in Figure 11-36. Type the proposed coefficients in the One-Way ANOVA Contrasts dialogue box, in order, from the first group. For example, we would enter μ1, μ1, +1, and +1 in order for our first example and +3, μ1, μ1, and μ1 for the second example. Note that you need to click on “Add” for each coefficient. Then, click “Continue” and proceed as you did with one-way ANOVA. This procedure will produce the output of requested planned contrasts. An example output for our first example is shown in Table 11-6. Results indicate that the mean health index for those who exercise 3 or 5 days per week is substantially higher than that for those who do not exercise or those who exercise only 1 day per week.

Selecting “Contrasts” in the One-Way ANOVA dialogue box in SPSS.

A screenshot in S P S S Editor shows the selection of Contrasts button in one-way ANOVA dialog box. The numerical data in the worksheet lists Exercise and Health values.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

The One-Way ANOVA Contrasts dialogue box in SPSS.

A screenshot in S P S S Editor shows the one-way ANOVA Contrasts dialog box. The numerical data in the worksheet lists Exercise and Health values.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

Table 11-6 Example Output of Planned Contrasts

Coefficients

Amount of Exercise

Contrast

None

1 Day per Week

3 Days per Week

5 Days per Week

1

-1

-1

1

1

Contrast Tests

Contrast

Value of Contrast

Std. Error

T

df

Sig. (2-tailed)

Health index

Assume equal variances

1

4.5459

2.02545

2.244

76

.028

Does not assume equal variances

1

4.5459

2.02545

2.244

54.767

0.29

Post hoc tests are used when you want to make comparisons after examining the data to determine what means are contributing the greatest amount of variance by comparing all possible pairs of means. Note that the number of possible pairs to compare increases as the number of groups increases. For example, there are three tests of mean pairs when there are three groups (i.e., 1 vs. 2, 1 vs. 3, and 2 vs. 3). However, this number increases to six when there are four groups to compare pairwise (i.e., 1 vs. 2, 1 vs. 3, 1 vs. 4, 2 vs. 3, 2 vs. 4, and 3 vs. 4). Many post hoc tests control for inflated Type I error. There are many post hoc tests available; however, we will only discuss the most commonly used. As shown in Figure 11-38, the post hoc tests are divided into two groups: those that assume homogeneity of variance and those that do not.

The first group is composed of tests that assume homogeneity of variance; most post hoc tests fall into this group. The most commonly used tests are the Bonferroni test, the Tukey test, and the Scheffe test. All these tests take steps to control Type I error inflation caused by conducting many comparisons. Either the Bonferroni test or the Tukey test is good when the number of comparisons is low, but the Tukey test is better when the number of comparisons is high (i.e., the number of comparisons is five or more).

The second group is composed of tests that do not assume homogeneity of variance, so they are useful when this assumption is violated. There are four different tests, but Dunnett’s C test is most commonly used for correcting the problem associated with Type I error.

To conduct post hoc tests in SPSS, click on the “Post Hoc” button in the One-Way ANOVA dialogue box, as shown in Figure 11-37. The post hoc dialogue box is seen in Figure 11-38; note that the two groups of post hoc tests are shown. Select one of the post hoc tests in the dialogue box, depending on whether you violate the assumption of homogeneity of variance, and then click “Continue” to proceed as you did with one-way ANOVA. Note that we will use Dunnett’s C test, as we violated the assumption of homogeneity of variance. This procedure will produce the output of requested post hoc tests. An example output is shown in Table 11-7. Results indicate that those who exercise 5 days per week have a substantially higher health index than those who do not exercise.

Selecting “Post Hoc” in the One-Way ANOVA dialogue box in SPSS.

A screenshot in S P S S Editor shows the selection of Post Hoc button in one-way ANOVA dialog box. The numerical data in the worksheet lists Exercise and Health values.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

The Post Hoc dialogue box in SPSS.

A screenshot in S P S S Editor shows the one-way ANOVA Post Hoc dialog box. The numerical data in the worksheet lists Exercise and Health values.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. "IBM SPSS Statistics software ("SPSS")". IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

Table 11-7 Example Output of Post Hoc Tests

(I) Amount of Exercise

(J) Amount of Exercise

Mean Difference (I μ J)

Std. Error

95% Confidence Interval

Lower Bound

Upper Bound

None

1 day per week

-2.50696

1.01379

-5.3576

.3437

3 days per week

-3.16939

1.14320

-6.3839

.0451

5 days per week

-3.88351a

1.37061

-7.7375

-0.296

1 day per week

None

2.50696

1.01379

-.3437

5.3576

3 days per week

-.66242

1.49126

-4.8556

3.5308

5 days per week

-1.37655

1.67198

-6.0779

3.3248

3 days per week

None

3.16969

1.14320

-.0451

6.3839

1 day per week

.66242

1.49126

-3.5308

4.8556

5 days per week

-.71412

1.75347

-5.6446

4.2161

5 days per week

None

3.88351a

1.37061

.0296

7.7375

1 day per week

1.37655

1.67198

-3.3248

6.0779

3 days per week

.71412

1.75347

-4.2164

5.6446

ap .05.

Reporting Planned Contrasts and/or Post Hoc Tests ⬆ ⬇

Report planned contrasts results as you would with independent samples t-test results. The following is a sample report of our first planned contrast, where we compare groups that exercise 3 days or more per week against those who exercise fewer than 3 days.

When reporting post hoc test results, the p-value of each comparison along with the corresponding group descriptive statistics should be reported, such as in this example reporting of a Dunnett C post hoc test:

One-way ANOVA with planned contrasts combined with post hoc tests is a very robust approach to testing hypotheses on a single dependent variable.

Choosing the Right Statistical Test ⬆ ⬇

Choosing the right statistical test depends upon the proposed research questions and consideration of factors such as the number of groups that will be compared. In group comparisons, the independent variable is often called the grouping variable. In the Kurnat-Thoma, Edwards, and Emery (2018) study, the independent variable was thermometry method (axillary, tympanic, and temporal). Now, be careful, as it is easy to confuse groups with variables. For example, if the independent variable was race (one independent variable) and participants were White, Black, or Asian (three groups), we might mistakenly think that there are three independent variables instead of a single grouping variable—race—with the three groups. When you are designing investigations or reading reports, it is a good practice to ask yourself, “What are the independent and dependent variables in this study?”

We must also determine whether the groups are independent or dependent, and this can be confusing. “Independent” refers to an investigation in which participants in one group are not also members of the other group. For example, if our grouping variable is age (20μ30, 31μ40, 41μ50), then participants may be found in only one of those groups; they cannot be simultaneously 30 and 31 years old. In contrast, “dependent” refers to an investigation of a single group of participants when we are comparing the group to itself.

Summary ⬆ ⬇

In this chapter, we have seen how to conduct statistical tests that make comparisons between means. The simplest statistic for comparing two means is the t-test. The t-test and its variations allow us to make comparisons between two groups on a single dependent variable that is measured at the interval or ratio level. When we need to make comparisons between more than two groups and conserve power, we turn to analysis of variance. One-way ANOVA allows us to make comparisons between three or more groups on a single dependent variable. Planned contrasts and post hoc tests are used to determine what groups are contributing to the significance when an overall group difference is found.

All these techniques share similar assumptions related to normality, independence, and homogeneity of variance. Tests of differences between means are most useful in descriptive comparative and experimental designs in which differences between groups are of interest.

Critical Thinking Questions ⬆ ⬇

  1. What statistical test would be most appropriate to examine differences between a sample mean and a population mean? Differences between men and women on exercise frequency? Differences between four ethnic groups on caloric intake?
  2. What does “homogeneity of variance” mean in relation to conducting a one-way ANOVA?
  3. How is the independent sample t-test different from the dependent sample difference test?
  4. What multiple comparison tests would be most helpful following analysis of variance?
  5. How does the number of groups influence the choice of a statistical test of difference?
  6. How would you report the following one-way ANOVA findings in APA style where an independent variable was nurses’ education level?
  7. How might you use the findings from the below ANOVA table in practice?

Self-Quiz ⬆ ⬇

  1. Suppose that you plan to compare SBP among three age groups: 50μ65, 66μ80, and 80 and older. What statistical test will be most appropriate?
    1. One-way ANOVA
    2. One-sample t-test
    3. Independent t-test
    4. Dependent t-test
  2. You are planning to test the effect of music therapy on chronic pain intensity among a single group of older adults in long-term care. What statistical test will be appropriate to determine if a difference on pain intensity is present before and after treatment in a single group?
    1. One-way ANOVA
    2. One-sample t-test
    3. Independent t-test
    4. Dependent t-test
  3. You find that there is a substantial mean difference among three different ethnic groups at risk of falls in a nursing home and want to find out which group differs specifically from which group. What procedure will help you determine such differences?
    1. Skewness and/or kurtosis
    2. Levene’s test for homogeneity
    3. Post hoc or planned contrast

Reference ⬆

Kurnat-Thoma, E., Edwards, V., &Emery, K. (2018). Axillary, tympanic, and temporal thermometry comparison in a community hospital pediatric unit. Pediatric Nursing, 44(5), 235μ246.