Why it is important to know if the value of one fraction is equivalent to (=), less than (<), or greater than (>) the value of another fraction?
- Estimating the correct answer is an important step in dosage calculation.
- Estimating involves comparing values.
- Comparing reduces accidental overdosage or underdosage.
When the numerator and the denominator are the same, the value equals one (1).
Example: Six (6) slices of a pizza cut into 6 equal parts is considered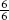 
(or 1) pizza (Figure 1-2).
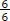of a pizza equals 1 whole pizza.
An illustration depicts a pizza divided into 6 equal slices.
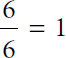
6 over 6 equals 1.
When the denominators are both the same, the fraction with the smaller numerator has the lesser value.
Example: Two (2) slices, or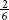 
of a pizza, are less than 3 slices, or 
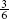of a pizza, of the same size (Figure 1-3).
An illustration depicts 2 pizzas divided into 6 equal slices. In the first diagram, 2 equal slices are cut off, and in the second diagram, 3 equal slices are cut off.
is less than 
ecause the denominators are the same and the numerator, 2 is less than the numerator, 3.
When the numerators are the same, the fraction with the smaller denominator has the greater value.
Example: If one pizza is sliced into 5 equal parts, and another same-sized pizza is sliced into 10 equal parts, each of the 10 slices will be smaller than the slices from the pizza cut into 5 pieces. So, 4 slices from the pizza cut into 5 pieces, or 
of a pizza, is a larger quantity than slices from the pizza cut into 10 pieces, or 
of a pizza.
is greater than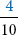 
because the numerators are the same, and the denominator, 5, is less than the denominator, 10 (Figure 1-4).
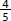(of a pizza), is a larger quantity than 
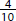(of a pizza), a fraction with the same numerator but a larger denominator.
An illustration depicts a slice cut off from a pizza with 5 equal slices on the left and 4 slices cut off from a pizza with 10 equal slices on the right.
When the numerators and denominators are different, to compare the fractions, do the following:
- Convert the fractions to equivalent fractions with a common denominator and then compare the numerators.
- To find a common denominator, multiply the numerator and denominator of the first fraction by the denominator of the other fraction.
- Next, multiply the numerator and denominator of the other fraction by the denominator of the first fraction, as demonstrated in the following examples.
Example 1: Determine if the first fraction is less than, greater than, or equal to the second fraction.
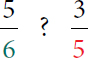
5 over 6, question mark, 3 over 5.
Find a common denominator:
- Multiply the numerator and denominator of the first fraction by 5 (the denominator of the second fraction).
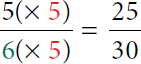
5, open parenthesis, times 5 close parenthesis over 6, open parenthesis, times 5 close parenthesis equals 25 over 30.
- Multiply the numerator and denominator of the second fraction by 6 (the denominator of the first fraction).
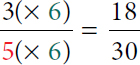
3, open parenthesis, times 6 close parenthesis over 5, open parenthesis, times 6 close parenthesis equals 18 over 30.
Compare the numerators of the resulting fractions,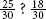 
. Because the numerator of the first fraction, 
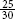, is larger than the numerator of the second fraction, 
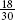, the first fraction has greater value:
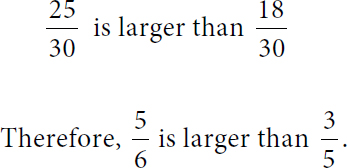
25 over 30 is larger than 18 over 30. Therefore, 5 over 6 is larger than 3 over 5.
Example 2: The patient had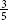 
of breakfast and 
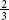of lunch. Did the patient eat more for breakfast or for lunch?
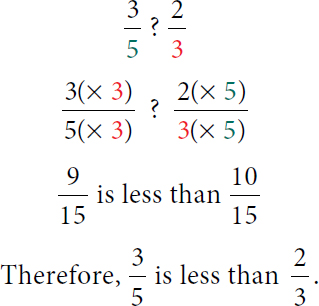
Calculation reads, 3 over 5, question mark, 2 over 3. 3, open parenthesis, times 3 close parenthesis, over 5, open parenthesis, times 3 close parenthesis, question mark, 2, open parenthesis, times 5 close parenthesis, over 3, open parenthesis, times 5 close parenthesis. 9 over 15 is less than 10 over 15. Therefore, 3 over 5 is less than 2 over 3.
So, the patient ate more for lunch.
Example 3: The patient walked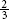 
of the hall in the morning and then 
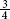of the hall in the evening. Did the patient walk farther in the morning or in the evening?
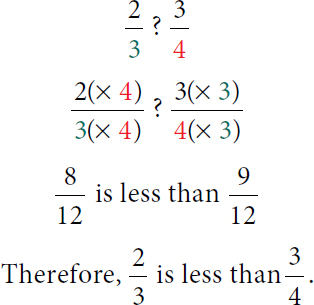
Determine if the patient walks farther in the morning or the evening.
Calculation reads, 2 over 3, question mark, 3 over 4. 2, open parenthesis, times 4 over 3, open parenthesis, times 4, question mark, 3, open parenthesis, times 3 over 4, open parenthesis, times 3. 8 over 12 is less than 9 over 12. Therefore, 2 over 3 is less than 3 over 4.
So, the patient walked farther in the evening.
If the denominators are large, find the least common denominator (LCD) by dividing the numerator and denominator of each fraction by a number that will yield the smallest denominator that is the same in both fractions.
Example: Determine if the first fraction is less than or greater than the second fraction.
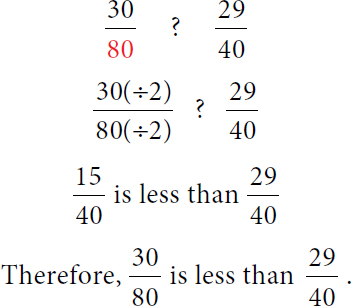
Calculation reads, 30 over 80, question mark, 29 over 40. 30, open parenthesis, divided by 2 over 80, divided by 2, question mark, 29 over 40. 15 over 40 is less than 29 over 40. Therefore, 30 over 80 is less than 29 over 40.
LEARNING ACTIVITY 1-2 Determine if the first fraction is less than, greater than, or equal to the second fraction.
1.
_______
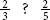2.
_______
3.
_______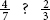