Dimensional analysis, also known as factor analysis or factor labeling, is an alternative way of solving mathematical problems. It's a basic and easy approach to calculating drug dosages because it eliminates the need to memorize formulas. Only one equation is required to determine each answer.

Factors are the main actors
When using dimensional analysis, a series of ratios, called factors, are arranged in a fractional equation. Each factor, written as a fraction, consists of two quantities of measurement that are related to each other in a given problem. Dimensional analysis uses the same terms as fractions, specifically the terms numerator and denominator.
Setting the stage
Let's say you want to change 48 inches to feet. The problem is written as follows:
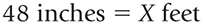
Some problems contain all of the information needed to identify the factors. You would just have to set up the equation, and find the solution. Other problems, such as this one, require a conversion factor.
Conversion factors are equivalents between two measurement systems or units of measurement. For example, 1 day equals 24 hours. In this case, day and hour are units of measurement and , when stated as 1 day = 24 hours, they're equivalent. This conversion factor can be used to solve problems involving the measure of time. There are many commonly used conversion factors. (See Common conversion factors.)
Putting it into practice
In the previous problem of how many feet are in 48 inches, use the conversion factor 12 inches equals 1 foot.
Because the quantities and unit of measurement are equivalent, they can serve as the numerator or denominator. The conversion can be written as:
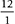
or
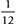
Setting up the equation
Solving a problem using dimensional analysis is like climbing a staircase—it requires steps. Six incredibly easy steps need to be followed to solve any problem. (See Following the steps.)
Stepping up to the problem
Let's take it one step at a time:
Given quantity—this is the beginning point of the problem. Identify the given quantity in the problem. In this case,
48 inches
Wanted quantity—this is the answer to the problem. Identify the wanted quantity in the problem as an unknown unit. In this problem it is:
X feet
Conversion factors—again, these are the equivalents that are necessary to convert between systems. The conversion factor for this problem is:
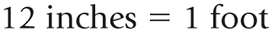
Set up the problem using necessary equivalents as conversion factors. When setting up equations, make sure that units you want cancelled out appear in both a numerator and a denominator. If an unwanted unit appears in two numerators, for example, you won't be able to cancel it. In this example, you want to cancel the inches and be left with the answer in feet. To do this, you must multiply 48 inches by a fraction that has inches in the denominator and feet in the numerator. The problem should be set up as:
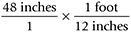
Just as with any type of mathematical problem, you'll cancel units that appear in both the numerator and denominator to isolate the unit you're seeking. In this case, you'll cancel inches, thereby isolating feet, which is the desired measurement. The step will look like this:
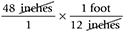
Multiply the numerators, multiply the denominators, and divide the product of the numerators by the product of the denominators to reach the wanted quantity.
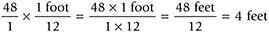
There are 4 feet in 48 inches.
Let's step to it again!
Now try to solve another problem using dimensional analysis. A package weighs 38 oz. How many pounds does it weigh?

Identify the given:
38 oz
Identify the wanted:
X lb
Identify the conversion factor:

Set up the equation:
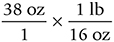
Cancel units that appear in both the numerator and the denominator:
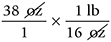
Multiply the numerators and denominators and divide the products:
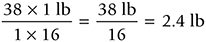
There are 2.4 lb in 38 oz.
Feel the conversion burn!
Now see how we can use dimensional analysis to take this same example a little further. If the same package weighs 38 oz, what does it weigh in kilograms?
Identify the given:
38 oz
Identify the wanted:
X kg
Identify the conversion factors (in this case, there are two):
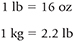
Set up the equation:

Cancel units that appear in both the numerator and the denominator:
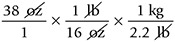
Multiply the numerators and denominators and divide the products:
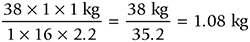
There are 1.08 kg in 38 oz.
Let's cool down…with one more rep!
Getting a good workout? Try one more to keep in peak shape. If you drank 64 oz of juice, how many cups of juice did you drink?
Identify the given:
64 oz
Identify the wanted:
X cups
Identify the conversion factor:
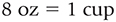
Set up the equation:

Cancel units that appear in both the numerator and the denominator:
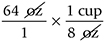
Multiply the numerators and denominators and divide the products:
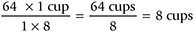
There are 8 cups in 64 oz.
Take a breath and let's review
Now that you've made it through the steps again, let's pause to study some key ideas. Dimensional analysis is a method of problem solving that can be used whenever two quantities are directly proportional to each other. One of the quantities can be converted to another unit of measurement by using common equivalents or conversion factors. The problem is treated as an equation using fractions. (See Quick guide to dimensional analysis.)

Now on your feet and do it again!
Apply the concepts you just reviewed above. Tom is recovering from arthroscopic surgery. As part of his rehabilitation, he walks one-half of a mile each day. If he usually walks at a pace of 1.5 miles per hour, how long will it take Tom to complete his walk?
Identify the given:
0.5 miles
Identify the wanted:
X hr
Identify the conversion factor:
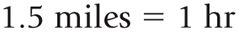
Set up the equation:
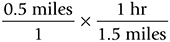
Cancel units that appear in both the numerator and the denominator:
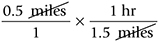
Multiply the numerators and denominators and divide the products:

It will take Tom 0.33 hours to complete his walk.
A patient is ordered to receive 70 mg of enoxaparin (Lovenox). It's available in vials that contain 30 mg per 0.3 mL. How much should be prepared?


Begin by identifying the given quantity:
70 mg
Then isolate what you're looking for:
X mL
Know your conversion factor:
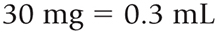
Set up the equation:
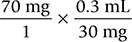
Identify and cancel units that appear in both the numerator and the denominator:
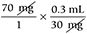
Lastly, multiply the numerators and denominators and divide the products:
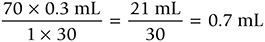
The patient would receive 0.7 mL of Lovenox.
Solve for Synthroid
A patient is to receive 50 mcg of levothyroxine (Synthroid). The drug is available as 200 mcg per 5 mL. How many milliliters should the nurse prepare?
The given quantity:
50 mcg
The wanted quantity:
X mL
The conversion factor:
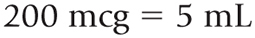
Set up the equation:
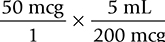
Cancel units that appear in both the numerator and the denominator:
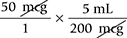
Then multiply the numerators and denominators and divide the products:
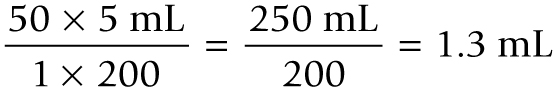
The nurse should prepare 1.3 mL of Synthroid.

How much heparin?
The doctor prescribes 10,000 units of heparin added to 500 mL of D5W at 1,200 units/hour. How many drops per minute should you administer if the IV tubing delivers 10 gtt/mL?
The given quantities (in this case, there are three):

The wanted quantity:

The conversion factor:
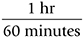
Set up the equation:

Cancel units that appear in both the numerator and the denominator:
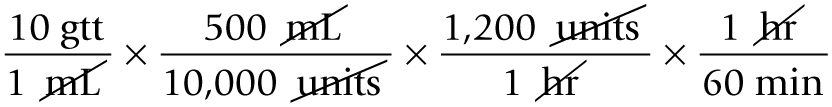
Then multiply the numerators and denominators and divide the products:
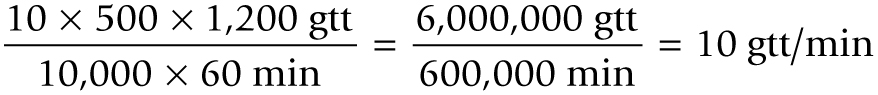
You should administer the heparin at a rate of 10 gtt/min.

Learning Lasix lingo
Let's try one more problem. Your patient is to receive 20 mg of furosemide (Lasix) oral solution. The bottle is labelled 40 mg per 5 mL. How many milliliters will the patient receive?
The given quantity:
20 mg
The wanted quantity:
X mL
The conversion factor:
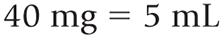
Set up the equation:
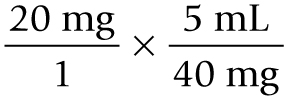
Cancel units that appear in both the numerator and the denominator:
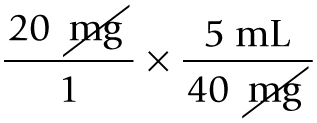
Multiply the numerators and denominators and divide the products:

The patient would receive 2.5 mL of Lasix oral solution.
