section name header

Learning Objectives ⬇

The principal goal of this chapter is to help you understand and use descriptive statistics with a normal distribution. This chapter will prepare you to:

Key Terms ⬆ ⬇

Introduction ⬆ ⬇

We have seen how nurses in practice, leadership roles, and research can present data and statistical analyses in graphs, charts, and tables. Because the data are presented more concisely, these visual displays are very useful, but we lose the details in these displays, especially around the distribution of data that are measured at the interval and ratio level (continuous variables). Additionally, visual displays may not be helpful with questions such as: “What is the average length of stay in a nursing home?”“What is the range of comorbid diagnoses among patients admitted to the medical intensive care unit?” or “What is the most frequently reported reason for patients coming to urgent care?” In combination with the visual representation of data, we also need an approach that allows exploration and understanding of the details. Descriptive statistics are used to communicate important information about the characteristics of the participants and phenomena in a study.

When the data are measured at the interval or ratio level, it is important to present the distribution of data in terms of central tendency (i.e., the average case) and variability (i.e., the range and spread of the data from the center). For example, Figure 6-1 shows a histogram of incomes of recent graduates in family nurse practitioner (FNP) programs. Questions we might ask about graduates are: “What would be the typical or average measurement value of a hypothetical person selected from this group?” and “How far are data values spread from the average?” These are difficult questions to answer with visual displays such as graphs, charts, and tables. We need numerical measures of central tendency and variability so that we can understand the distribution of the data on an objective basis. Descriptive statistics are numeric measurements of central tendency and variability, and they help us explain the data more accurately and in greater detail than visual displays alone.

Histogram of incomes of recent graduates in FNP programs.

A histogram shows the incomes of recent graduates in family nurse practitioner programs.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. “IBM SPSS Statistics software (“SPSS”)”. IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

Data may be distributed in many different ways, depending upon where the average is located and how far the data values are spread from that average (variability). The center of the distribution can be located in the middle, or it may be shifted to the left or right. The data can present with a high peak, where most of the data values are close to each other, or the peak may be low and the data points spread far apart. In this chapter, you will learn how to compute and interpret measures of central tendency and variability. Three common measures of central tendency—mode, median, and mean—will be explained first. Then, we discuss the four common measures of variability—range, interquartile range, variance, and standard deviation. We will also explain the use of descriptive statistics for understanding normal distributions. In normal distribution, the percentages of data values are equally dispersed from the center of the distribution. Many statistical procedures that we will discuss, in later chapters, assume that the data follow normal distribution.

CASE STUDY
Data from Johnson, K., Razo, S., Smith, J., Cain, A., & Soper, K. (2019). Optimize patient outcomes among females undergoing gynecological surgery: A randomized controlled trial. Applied Nursing Research, 45, 39-44.

In 2019, Kari Johnson and colleagues published a study evaluating if length of stay, readmission rates, and patient satisfaction changed after implementing an evidence-based education bundle for female patients having gynecological surgery, as compared with standard care (Johnson et al., 2019). A team of nurses, physical therapists, and a surgeon developed the education bundle based on the best evidence available. They used a prospective, comparative, and randomized design to test the patient education intervention in a 28-bed medicalμsurgical unit at a community hospital.

The authors used two tables to describe key demographics and variation in the groups. The first table shows the side-by-side numeric data for the education bundle and the standard education participants. The reported characteristics are age groupings ( 50, 51-64, 65-74, 75-84), race (Caucasian, non-Caucasian), marital status (married, divorced, single, widowed), and tobacco use (yes, no). All variables in both groups have a sample size of 25 participants (n = 25). In the instance of tobacco use, the demographic data for both the intervention group and control group was yes = 2 and no = 23.

In the second table, the groups are compared for each category to demonstrate if they are similar by using sample size (n), mean (M), and standard deviation (SD). For example, the statistical data in this table for the variable of age is

  • Education bundle; n = 25, M = 2.36, SD = 0.907
  • Standard education; n = 25, M = 2.24. SD = 0.969

Although these tables do not tell us if the education bundle was superior to standard education for patients who had gynecological surgery, it does provide helpful information to determine if it is reasonable to compare these groups who received the education bundle or standard care.

Measures of Central Tendency ⬆ ⬇

We often encounter descriptions of central tendency, or averages, in newspapers and journal articles. Here are few typical examples.

Mean age at index date was 83.2 years (SD = 7.2) among cases and 83.7 years (SD = 7.2) among controls (Morin et al., 2019)

In the total sample of patients with actigraphs, the mean age was 85.5 years (SD = 7.3), 76% were female, the mean Cornell Scale for Depression in Dementia (CSDD) score was 11.2 (SD = 3.7), the mean Mini-Mental State Examination (MMSE) score was 7.6 (SD = 6.0), the mean Mobilization-Observation-Behaviour-Intensity-Dementia-2 (MOBID-2) score was 2.8 (SD = 2.1), and 54.7% had a MOBID-2 score ≥ 3 (Blytt et al., 2018).

These authors all used a single number to describe an important aspect of data—an average. There are multiple ways of computing and presenting averages, but we will describe the three most common measures of central tendency: mode, median, and mean.

The Mode

The mode is simply the most frequently occurring number in a given data set. Let us examine the following data set of seven systolic blood pressure (SBP) measurements:

120 114 116 117 114 121 124

Notice that 114 appears twice and all other measurements appear only once. Therefore, the SBP measurement of 114 is the mode in this data set because it is the most frequently occurring value. This particular distribution of SBPs may be described as a unimodal distribution because there is only one mode. However, it is possible to have more than one mode in a data set. To explain, let us examine the following data set:

117 120 114 116 117 114 121 124

This data set has two modes, 114 and 117, because they each appear twice and the others appear only once. A data set with two modes is a bimodal distribution, and a multimodal distribution is a distribution with more than two modes.

As you probably noticed, the mode is useful primarily for variables measured at the nominal level because it is merely the most frequently occurring number in the data set. For example, if we have assigned the following numbers to the sex of participants, 1 for male and 2 for female, and out of a sample of 100 there are 75 females, the mode is 2. The mode will not be useful with continuous levels of measurement, or as the data set gets larger.

The Median

The median is the exact middle value in a distribution and divides the data set into two exact halves. Let us consider the following data set that consists of five income levels for registered nurses:

35,000 39,500 42,000 47,500 52,000

In this data set, the value of 42,000 is the median, because it divides the data set into exactly two halves, with an equal number of values below and above it. It was easy to find the median in this data set, but notice that this data set is ordered from the smallest to the largest data value. Finding the median may be difficult and misleading if the data values are not ordered consecutively. Consider the following data set:

47,500 39,500 32,000 52,500 42,000

It will not make sense to choose 32,000 and report it as the median, because it is the smallest data value in this data set. Therefore, ordering the data from the smallest to the largest (or vice versa) is the first and the most important step in finding the median of any given data set. After ordering the values, it is easy to see that the median for this data set should be 42,000.

Notice also that the previous two data files had odd numbers of data values. Finding the median in a data set with an odd number of values is easy because you will end up with an equal number of data values above and below the median. However, it is more challenging to find the median when there are an even number of data values in the data set. Consider the following data set:

24 29 32 35 39 40

The data values represent age in years of six individuals, and there is no number that divides this data set into two exact halves. Theoretically, such a number should be between 32 and 35, leaving three data values above and below it. However, such a number does not actually exist in the data set. In this case, you must calculate the median by summing the two middle numbers, 32 and 35, and dividing the sum by 2. You are basically computing the average of those two middle values as the median, as follows:

Remember that we still must order the data from the smallest to the largest value before finding a median.

The Mean

The arithmetic mean (often called the average) is the sum of all the data values in a data set divided by the number of data values and is shown in the following equation:

The mean involves the mathematical operations of addition and division, and so is an appropriate measure of central tendency for interval and ratio levels of measurement. For example, we might use it to calculate an average of a patient’s SBP over time to determine the effect of medication. However, it is not possible to find a meaningful interpretation for an arithmetic mean for the categorical, or nominal, variable, such as political affiliation, with categories of Republican, Independent, and Democratic. Let us consider the following data set of sodium content levels, measured in milligrams per liter:

20 18 16 22 27 11

For this data set, the mean will be:

We have computed a mean of 19 for a group of six sodium content levels. How should we interpret this finding? Remember that the mean is the average score in the data set. Therefore, the mean tells us that, on average, the sodium content level in this data set is 19 mg per liter.

Choosing a Measure of Central Tendency

We have discussed three types of central tendency—the mode, the median, and the mean—and examined how they differ in terms of finding the center of a data distribution. The next legitimate question is, “When do we use which measure?”

The mode is simply the most frequently occurring data value(s) in the data set. Therefore, it is mainly useful for variables at the nominal level of measurement. Both median and mean are useful when the variable being measured can be quantified at the interval or ratio level. However, one important thing to note here is that the mean is extremely sensitive to unusual cases. To explain this further, let us consider the following data sets:

Data set #1: 108 112 116 120 124

Data set #2: 108 112 116 120 205

In both data sets, the median is 116, as it is the number that divides the data set into two exact halves. However, you will notice that the mean is not identical in both data sets.

For the first data set, the mean is equal to:

whereas the mean of the second data set is equal to

Notice how the mean of the second data set has been influenced by the presence of an unusual case in the data set. If we were to say that the mean is equal to 132.2 for the second data set and it represents a typical case, this will not make much sense because the majority of data values are less than 120. Therefore, the mean should not be used when unusual, or outlying, data values are present in the data set, as the mean tends to be extremely sensitive to the unusual values. Rather, the median should be reported in this case. This is why the average housing price is always reported with the median, because even a single million-dollar house can distort the average housing price when most of the houses are in the range of $200,000 to $350,000.

Measures of Variability ⬆ ⬇

Measures of central tendency allow us to know the typical value in the data set. However, we know that when we measure a variable, there will be differences between and among the values in the data set. For example, if we were measuring SBP among a group of research participants, we would expect that there would be a range of values among individuals. Furthermore, we would also expect similar variations on SBP measurements over different times in any individual participant. In other words, some level of variation among data values in any data set is expected. Our understanding of the characteristics of the data is enhanced when we also understand the nature of variability in the data set. For example, if a sample of patients has a mean SBP of 130 mm and most patients are within 10 mm of that value, then that data set will look very different than if most patients are within 50 mm of the mean. Whenever we measure central tendency, we also need to calculate variability to achieve a thorough grasp of the data.

We also use measures of variability to provide information about how well a measure of central tendency represents the “middle/average” value in the data set. The computed measure of central tendency will be most accurate when the data values vary only a little, but accuracy of the mean declines as the variation in data values increases. There are multiple ways of computing and presenting variability, but we describe the four that are most commonly used: range, interquartile range, variance, and standard deviation.

Range

Range is simply the difference between the largest and the smallest values in the data set. For example, suppose that a researcher measured patients’ level of pain after vascular surgery on a scale of 0 to 10. These data set is:

9 3 2 6 7 8 7 5

The first step is to sort the data from the smallest to the largest values, as it will make our job of finding these two values easy. After sorting, the range of this data set is 9 - 2 = 7.

Range is simple to calculate. As seen in the previous example, the range is calculated simply by subtracting the smallest value from the highest value. However, we should be cautious about using range as a measure of variability, as it only uses the highest and lowest values in computation. In other words, the range is extremely sensitive to unusual data values. Therefore, it does not accurately capture information about how data values in the set differ if the data set contains an unusual value(s).

Consider the following data set:

3 4 2 3 3 4 2 9

This data set is still a collection of pain level measurements of patients who underwent vascular surgery, but notice that the value of 9 seems unusual in this data set. Here, the range is 9 - 2 = 7 after sorting. Does this make sense? Most of the values are between 2 and 4, and claiming that the variability is 7 does not really make sense in the context of this data set. To get around this problem, sometimes researchers will simply report the range as the lowest and highest values, “reports of pain intensity ranged from 3 to 9,” rather than computing a range.

Interquartile Range

Interquartile range is the difference between the 75th percentile and 25th percentile. Percentile is a measure of location and tells us how many data values fall below a certain percentage of observations. Therefore, the 25th percentile is the data value that the bottom 25% falls below, and the 75th percentile is the data value that the bottom 75% falls below. In results, the interquartile range is less sensitive to an unusual case(s) in the data set, as it does not use the smallest and the largest values as the standard range. For example, suppose the number of patient falls per week at a local nursing home have been measured:

1 1 2 2 2 3 3 3 4 4 5

Note that the data set has already been sorted from the smallest to the largest. It is easier to find the median first, and then to find the 25th and 75th percentiles, because it is more difficult to directly identify the percentiles.

The median of this data set is 3, because 3 is the middle value that divides this data set into two exact halves. From the median, the 25th percentile is equal to 2 and the 75th percentile is equal to 4, as they divide the lower and upper halves of the data set into two exact halves. The interquartile range is then the difference between the 25th percentile and the 75th percentile, which is 4 - 2 = 2.

Let us now consider the next data set:

1 1 2 2 2 3 3 3 4 4 24

As you can see, it is the same data set as before, except for the highest value, 24, which seems to be an unusual value. Notice that the interquartile range is still 4 - 2 = 2 and is not affected by the unusual data value. Therefore, interquartile range is less sensitive to unusual or outlying values.

Variance and Standard Deviation

Although range provides a rough estimate of the variability of a data set, it does not use all of the data values in computation and is very sensitive to an unusual value in the data set. Interquartile range is an improvement, but it still does not account for every data value in the set. On the other hand, the next two measures of variability, variance and standard deviation, use all of the data values in the set when computing variability and may capture information about variability more precisely than the range or the interquartile range. As standard deviation is simply the square root of variance, we will explain variance first.

Variance is the average amount that data values differ from the mean and is computed with the following formulas:

In this equation, we compute the difference between each raw value and the mean (X -

X

, square the result, sum (Σ) those values, and then divide by the total number of values in the data set (N). Note that the denominator will be changed to n - 1 when working with samples.
Degrees of Freedom

Calculations of variance and many other statistics require an estimate of the range of variability, known as degrees of freedom. From a sample, degrees of freedom are always equal to n - 1. Here is an analogy that might help you understand degrees of freedom. Envision a beverage holder from any fast food restaurant—most of these hold four drinks. In this case, the degrees of freedom would be equal to 4 - 1, or 3. As each section of the holder is occupied by a drink, there is a chance of varying in what section of the holder any given drink is placed, top left or top right for example, until three of the sections are filled; at this point, there is only one section left where a drink may be placed, and no variation is possible. Each statistical test or calculation has a variation of degrees of freedom. Watch for these throughout the text.

To compute variance, let us consider the following data set of toddler weights in an outpatient clinic, assuming that the data values were taken from a population:

19 22 24 26 19

The computation steps are shown in Table 6-1.

Table 6-1 How to Compute the Variance

A table is titled how to compute the variance.

Computed variance for this data set is 7.6. What does this mean? Recall that the values represent toddler weights in an outpatient clinic, measured in pounds. Because the deviation of each observation from the mean has been squared, the unit for the variance is now in (pound)2. What does (pound)2 mean? If we were to say that data values differ from the mean on average about 7.6 (pound)2, would this claim make sense? The claim probably does not make sense because there is no such unit as (pound)2.

Why do we then take the square of the deviation if the (unit)2 will not make sense to interpret at the end? The answer is simple: If you do not square the deviation and sum each deviation, it will always add up to zero, no matter what data set you work with. We suggest that you try this with small data sets in this text or other sources.

How can we then talk about variability if the measure of variability turns out to be equal to zero? This is why we take the square of the deviation to compute the variance first, and then take the square root of it that result compute the standard deviation, bringing us back to the original unit of measurement.

We get the standard deviation of 2.76 by taking the square root of 7.6; we can then say that the data values differ from the mean (22 pounds) on an average of about 2.76 pounds. We can interpret this finding to mean that, on average, about two-thirds of the weights fall between 19.24 and 24.76 pounds. This makes more sense when you look at the data set compared with the variance. Note that the mean and standard deviation should always be reported together!

Choosing a Measure of Variability

We have shown you how to compute four measures of variability—range, interquartile range, variation, and standard deviation—and how they differ. The next question to ask is, “When do we use which measure?”

You should use the range only as a crude measure because it is extremely sensitive to unusual values in the data set. Interquartile range is not as sensitive to unusual data values, and standard deviation is very sensitive to unusual values. Therefore, the interquartile range should be used with the median when the data contain unusual data values. However, the standard deviation should be used with the mean when the data are free of unusual data values.

Obtaining Measures of Central Tendency and Variability in Excel

In order to explain how to analyze the data in Microsoft Excel, we will first explain how to enable and use the Data Analysis ToolPak. Go to File > Options, as shown in Figure 6-2. Then, click on the Add-In category, select Excel Add-Ins in the Manage box, and click “Go,” as shown in Figure 6-3. Next, check the Analysis ToolPak check box in the Add-Ins box and then click OK (Figure 6-4). Now you should see the “Data Analysis” ToolPak under the Data pull-down menu (Figure 6-5).

Selecting the Option in Excel.

A screenshot shows a window with the Options tab in Excel highlighted.

Courtesy of Microsoft Excel © Microsoft 2020.

Selecting Excel Add-ins in Excel.

A screenshot of the Excel Add-ins lists the names of the Add-ins, location, and type. Below are information on the Add-ins: name, publisher, compatibility, and description, like, provides data analysis tools for statistical ad engineering analysis.

Courtesy of Microsoft Excel © Microsoft 2020.

Selecting the Analysis ToolPak from the Add-in list in Excel.

A screenshot shows the selection of Analysis ToolPak from the list of Add-ins, with its description below—Provides data analysis tools for statistical and engineering analysis. The buttons, O k, Cancel, Browse, Automation, are on the right of list.

Courtesy of Microsoft Excel © Microsoft 2020.

Data Analysis ToolPak shown in Excel.

An Excel screenshot shows the Data Analysis ToolPak in the Analysis group under Data menu in the menu bar.

Courtesy of Microsoft Excel © Microsoft 2020.

To obtain measures of central tendency in Excel, open Weight.xlsx and go to Data > Data Analysis and select “Descriptive Statistics” from the Analysis Tools list in the Data Analysis dialog box (Figure 6-6). Then, click “OK”. In the Descriptive Statistics dialog box, enter A1:A159 as the Input Range, check Labels in the first row, Summary Statistics, Kth Largest, and Kth Smallest (Figure 6-7). Clicking “OK” will then produce the output, as shown in Figure 6-8.

Selecting Descriptive Statistics in the Data Analysis dialog box in Excel.

An Excel screenshot shows a dialog box with heading, Data Analysis, and a list of options, of which Descriptive Statistics is selected. The buttons O k, Cancel, and Help are on the right of the dialog box.

Courtesy of Microsoft Excel © Microsoft 2020.

Defining options in the Descriptive Statistics dialog box in Excel.

An Excel screenshot shows the Descriptive Statistics dialog box with fields to define data. The data in the worksheet has the column heading, Weight, with a list of numerical data.

Courtesy of Microsoft Excel © Microsoft 2020.

Example output of descriptive statistics in Excel.

An Excel screenshot shows the output of weight from the descriptive statistics.

Courtesy of Microsoft Excel © Microsoft 2020.

Obtaining Measures of Central Tendency and Variability in IBM SPSS

There are several places in SPSS where you can request measures of central tendency and variability. To obtain these measures, open Weight.sav and go to Analyze > Descriptive Statistics. In the next menu, choose “Frequencies” (Figure 6-9).

Selecting the frequencies window in SPSS.

A screenshot in S P S S shows the selection of the Analyze menu, with the Descriptive Statistics option chosen, from which the Frequencies option is selected. The data in the worksheet has the column heading, Weight, with a list of numerical data.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. “IBM SPSS Statistics software (“SPSS”)”. IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

Move the variable(s) of interest, as shown in Figure 6-10. Of the three buttons on the right side of the window, select “Statistics” (Figure 6-11). You can select measures of both central tendency and variability to obtain the measures to suit your needs.

The Frequencies window in SPSS.

A screenshot in S P S S shows the Frequencies dialog box.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. “IBM SPSS Statistics software (“SPSS”)”. IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

The statistics button in the Frequencies window.

A screenshot in S P S S shows the Frequencies: Statistics dialog box.

Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. “IBM SPSS Statistics software (“SPSS”)”. IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.

The same measures can be obtained by choosing “Descriptives” or “Explore” under the Analyze > Descriptive Statistics pull-down menu. Note also that these measures of central tendency and variability can be obtained within windows for several other statistical procedures.

Normal Distribution ⬆ ⬇

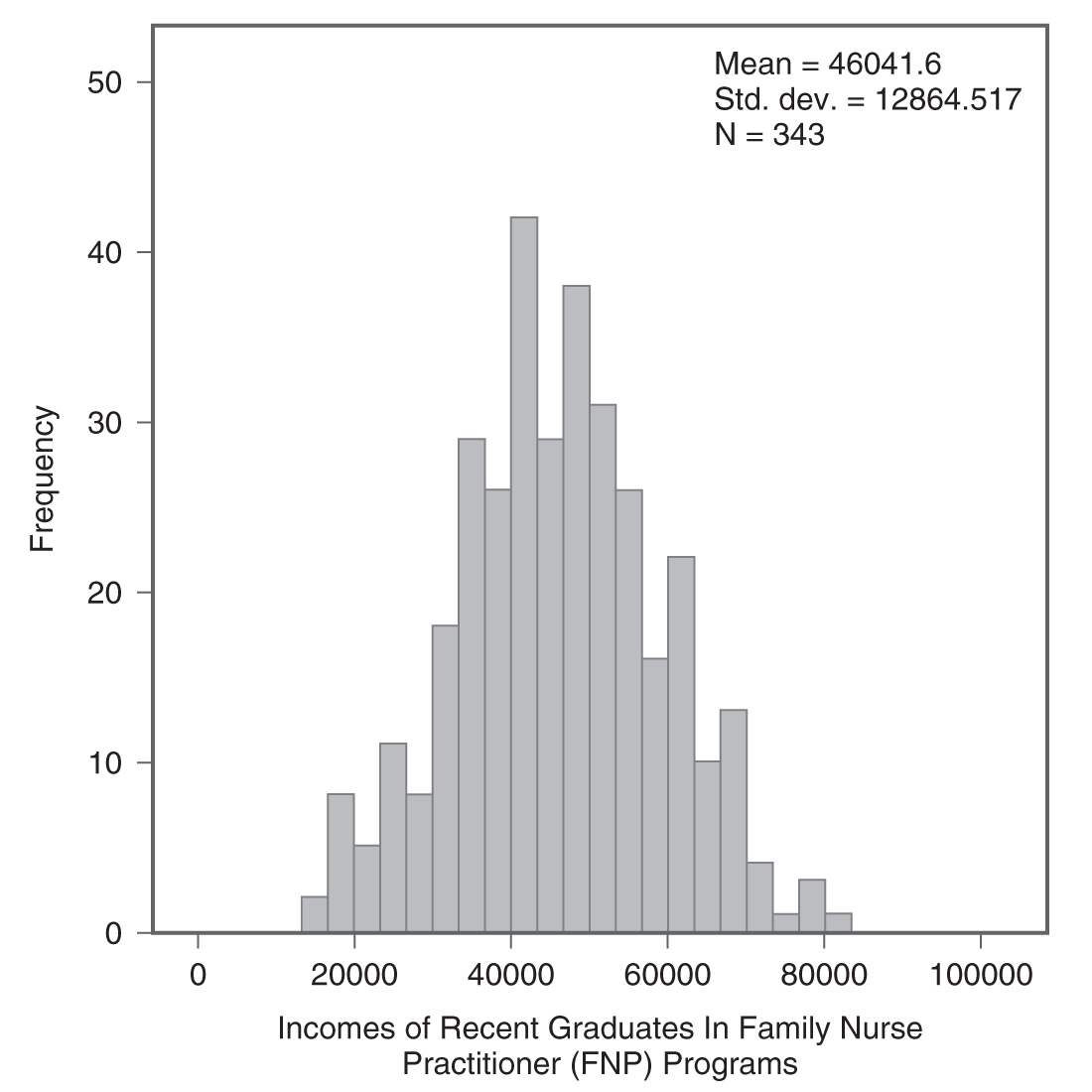
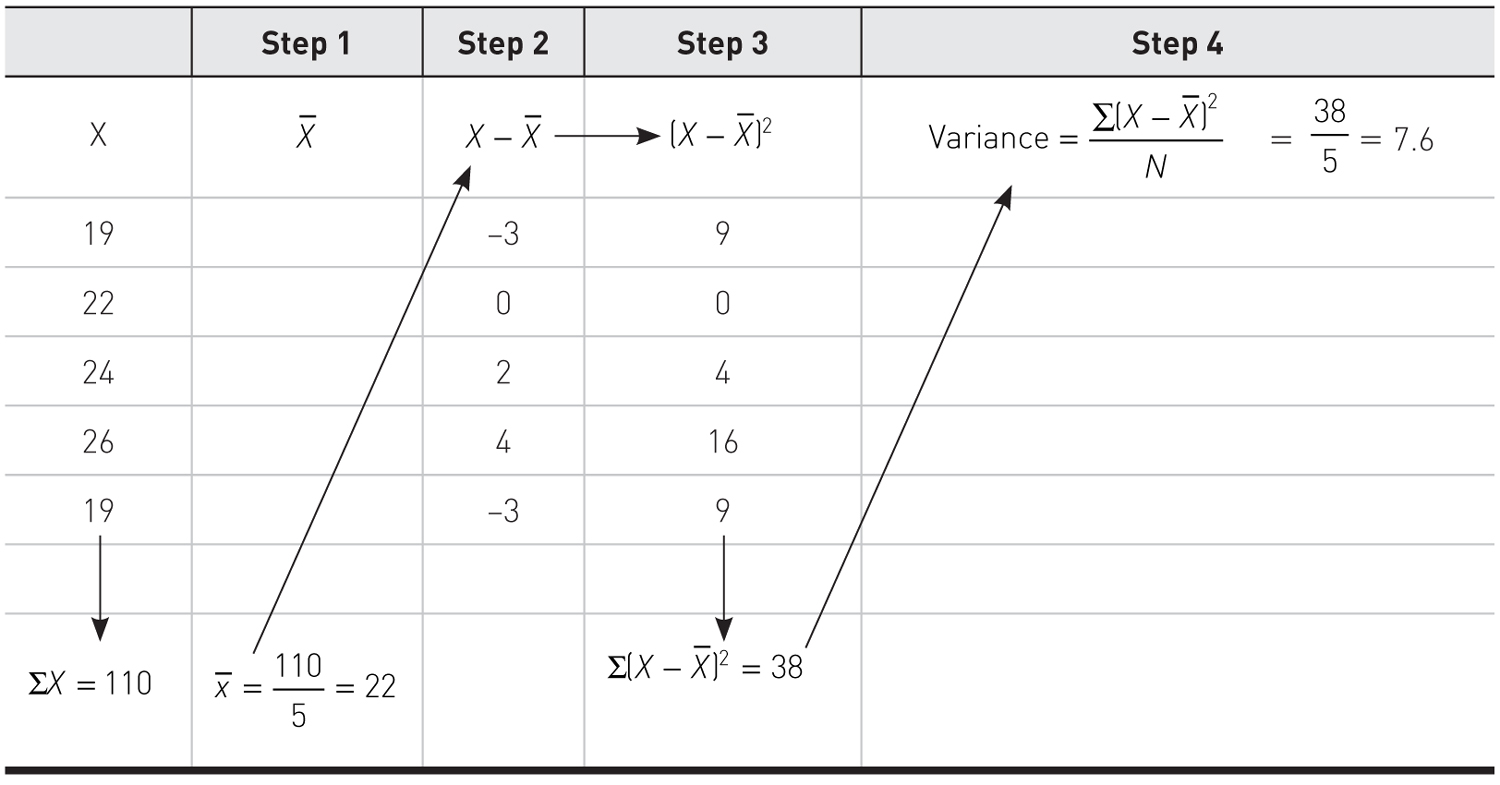
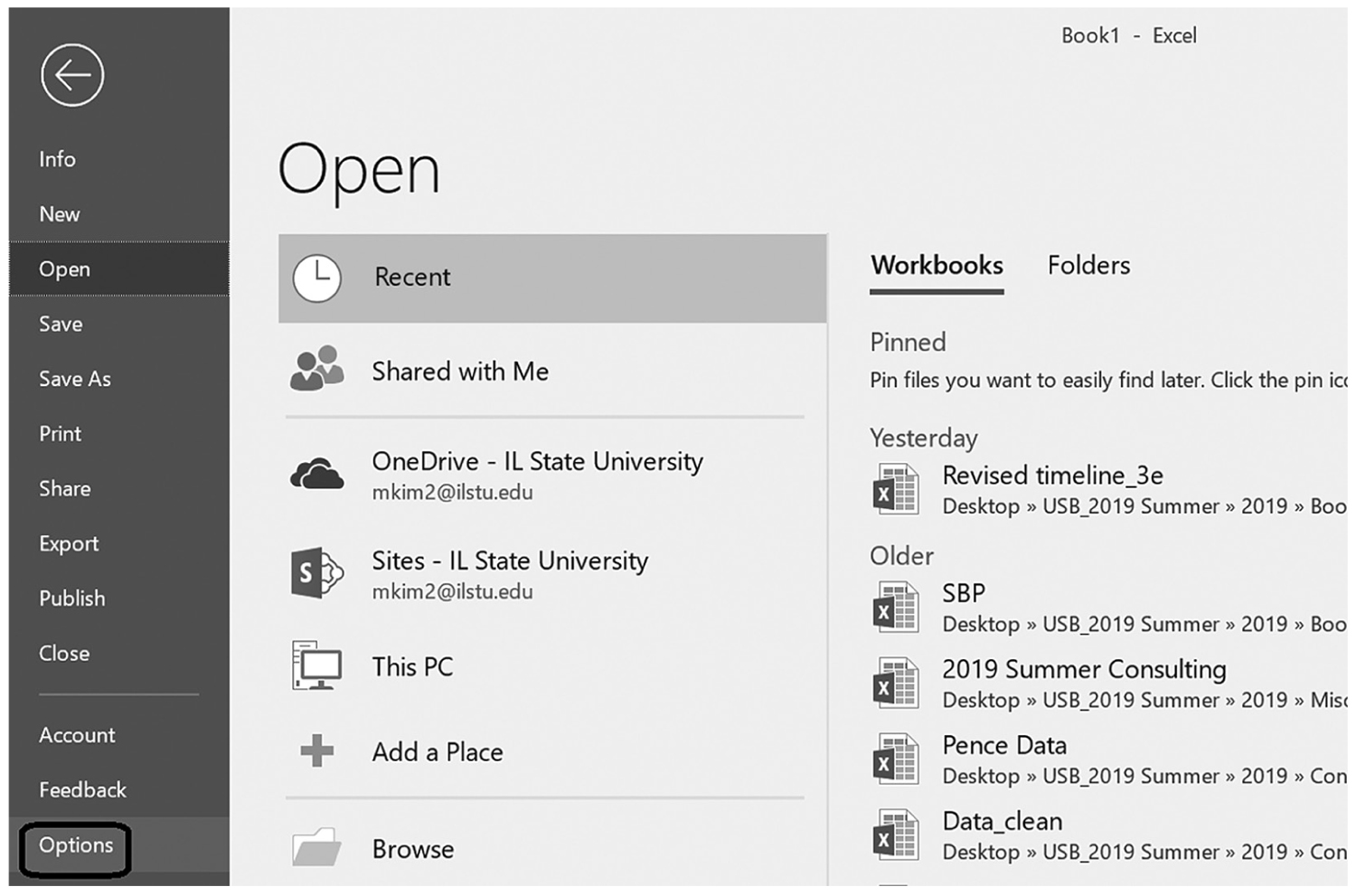
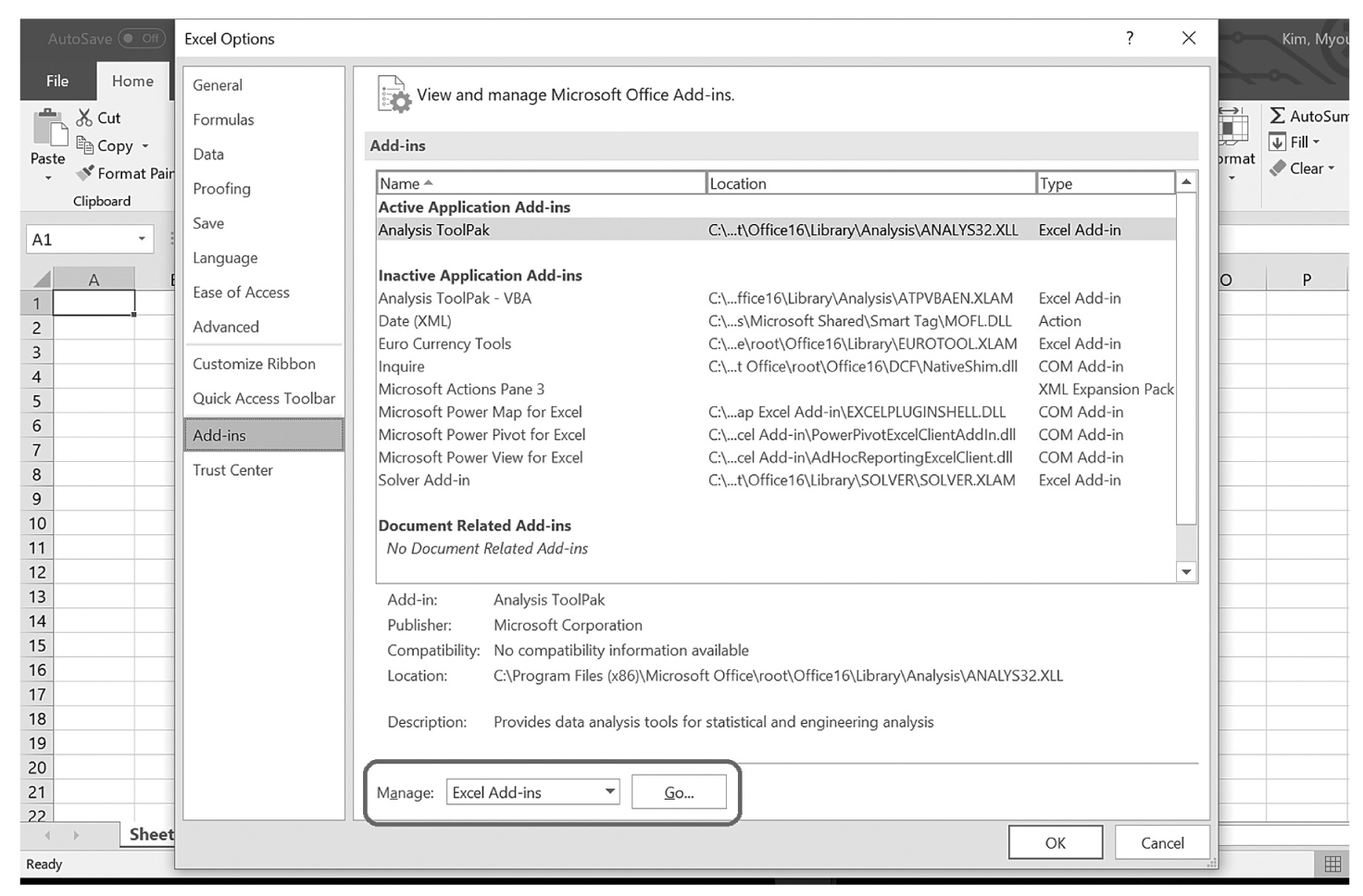
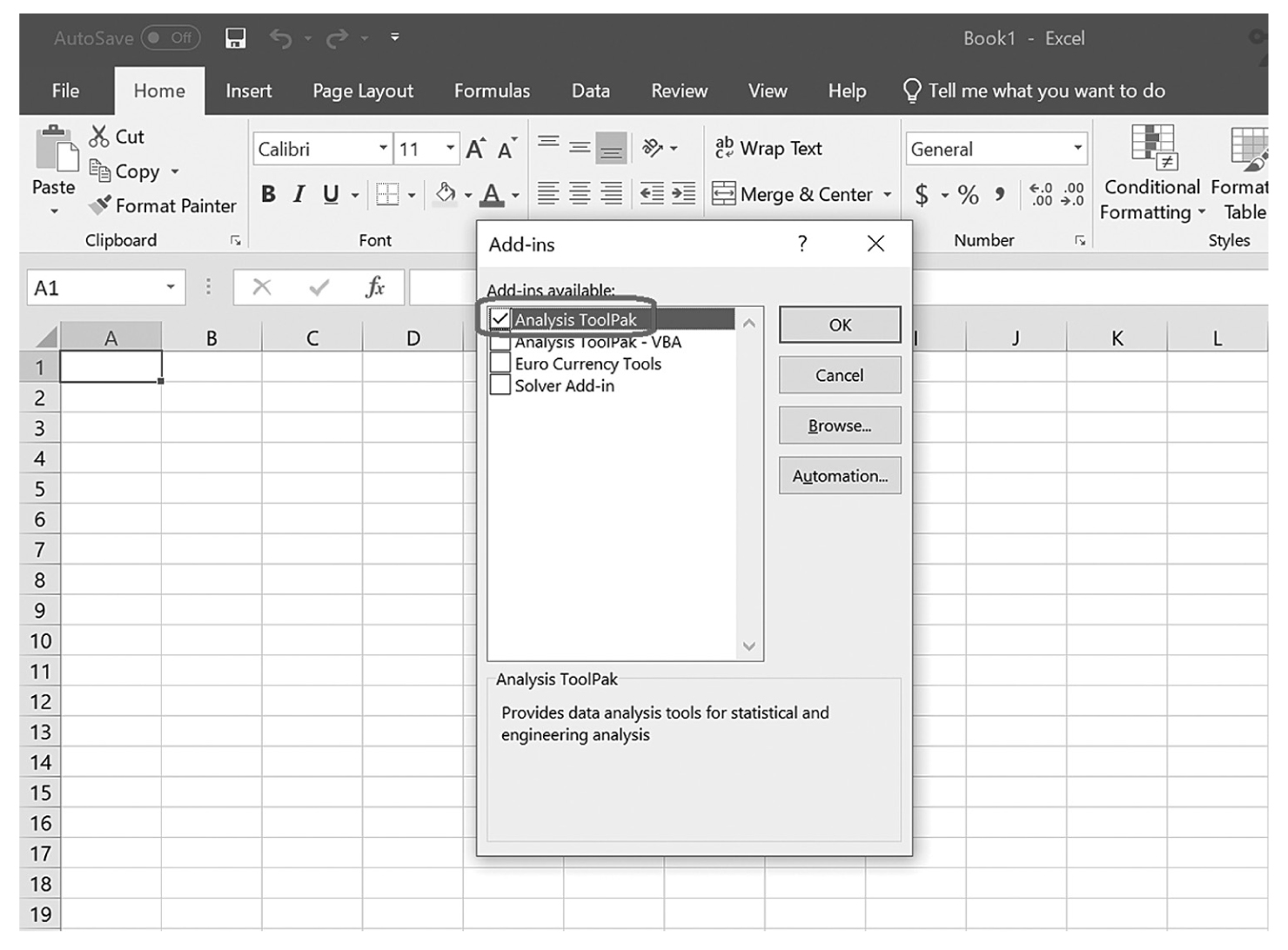
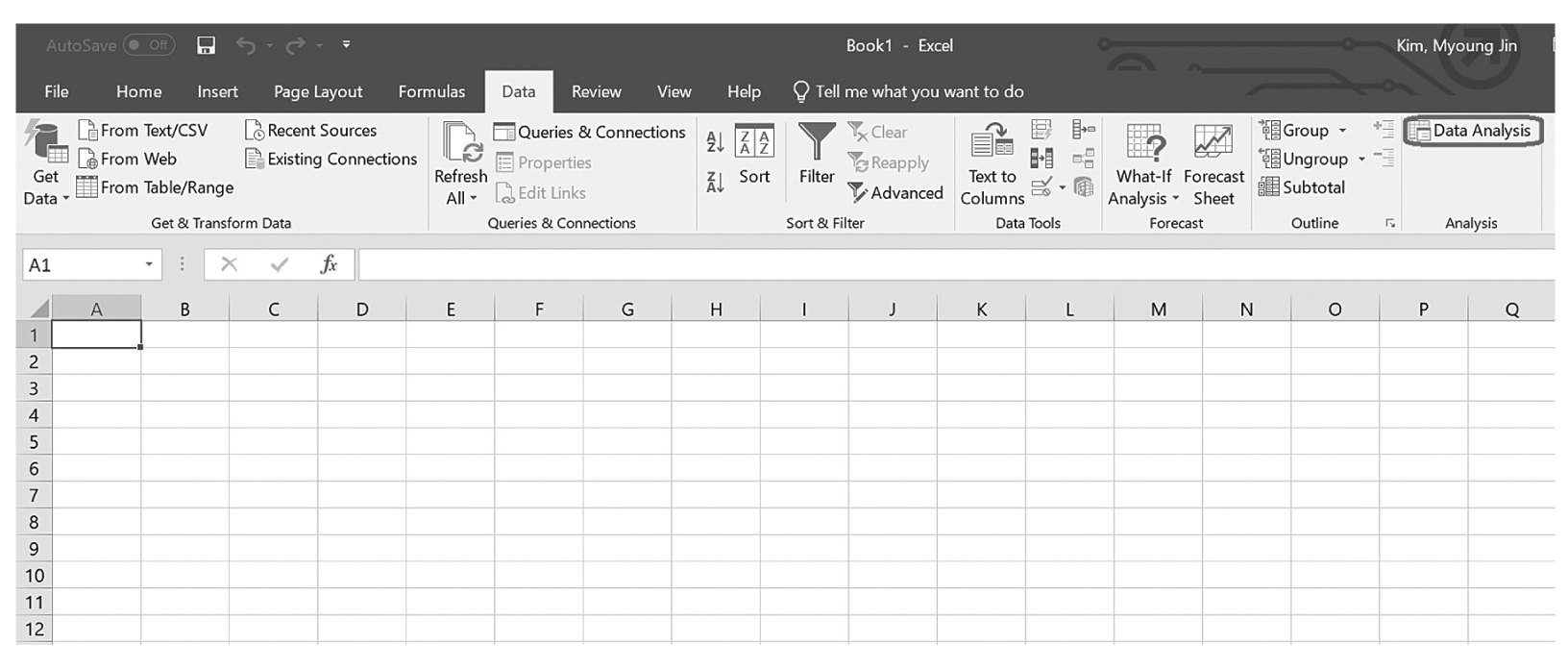
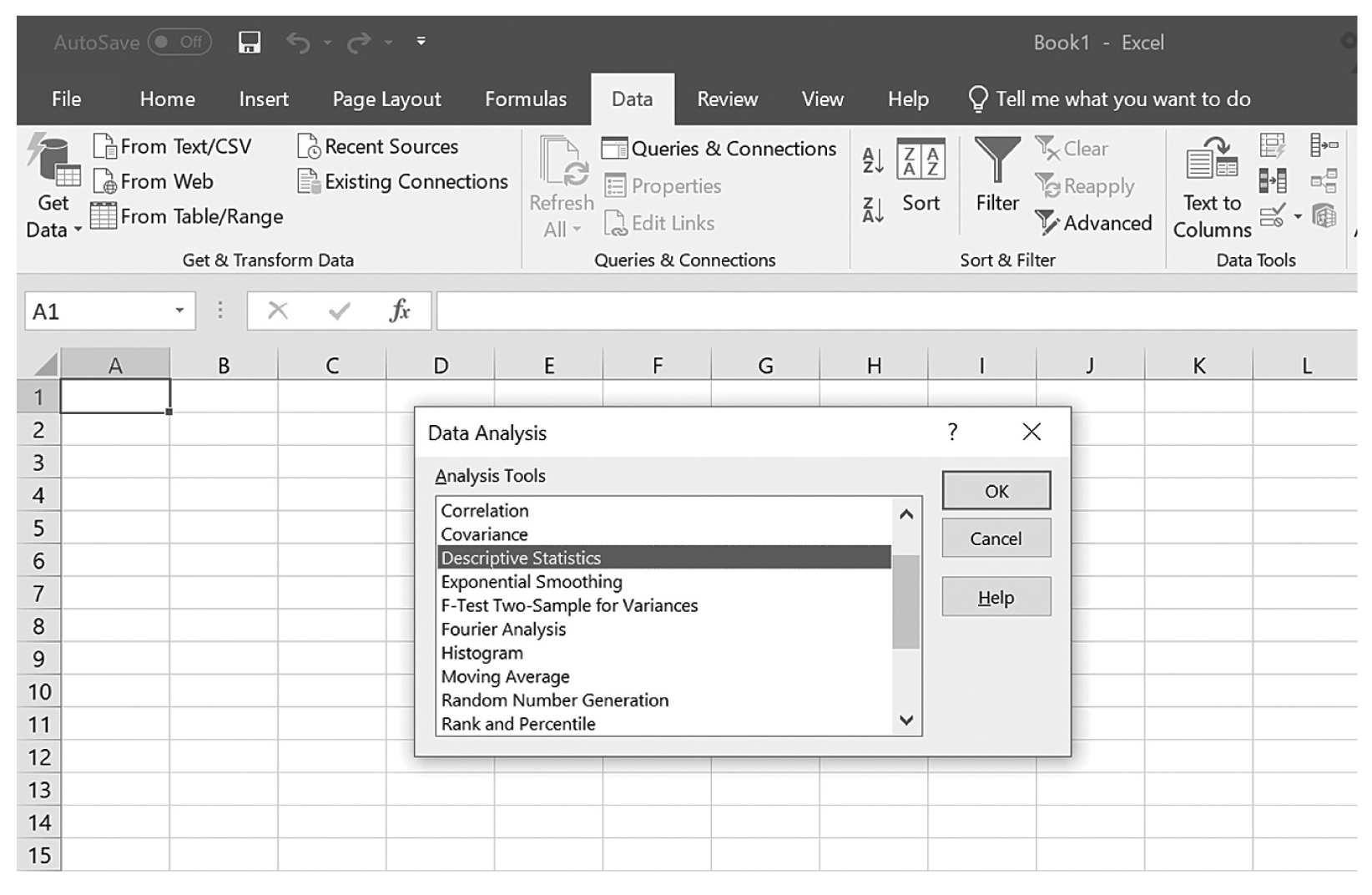
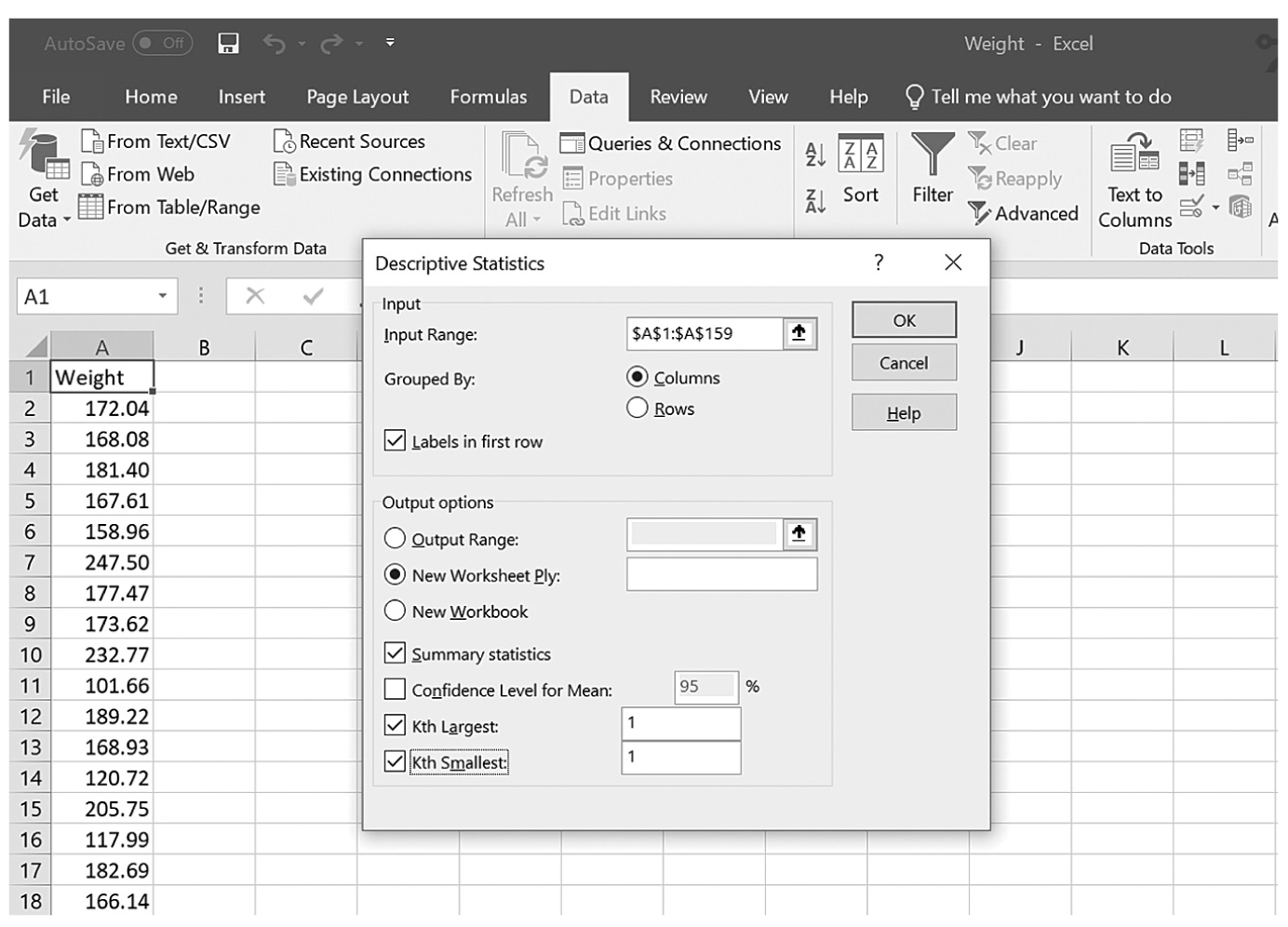
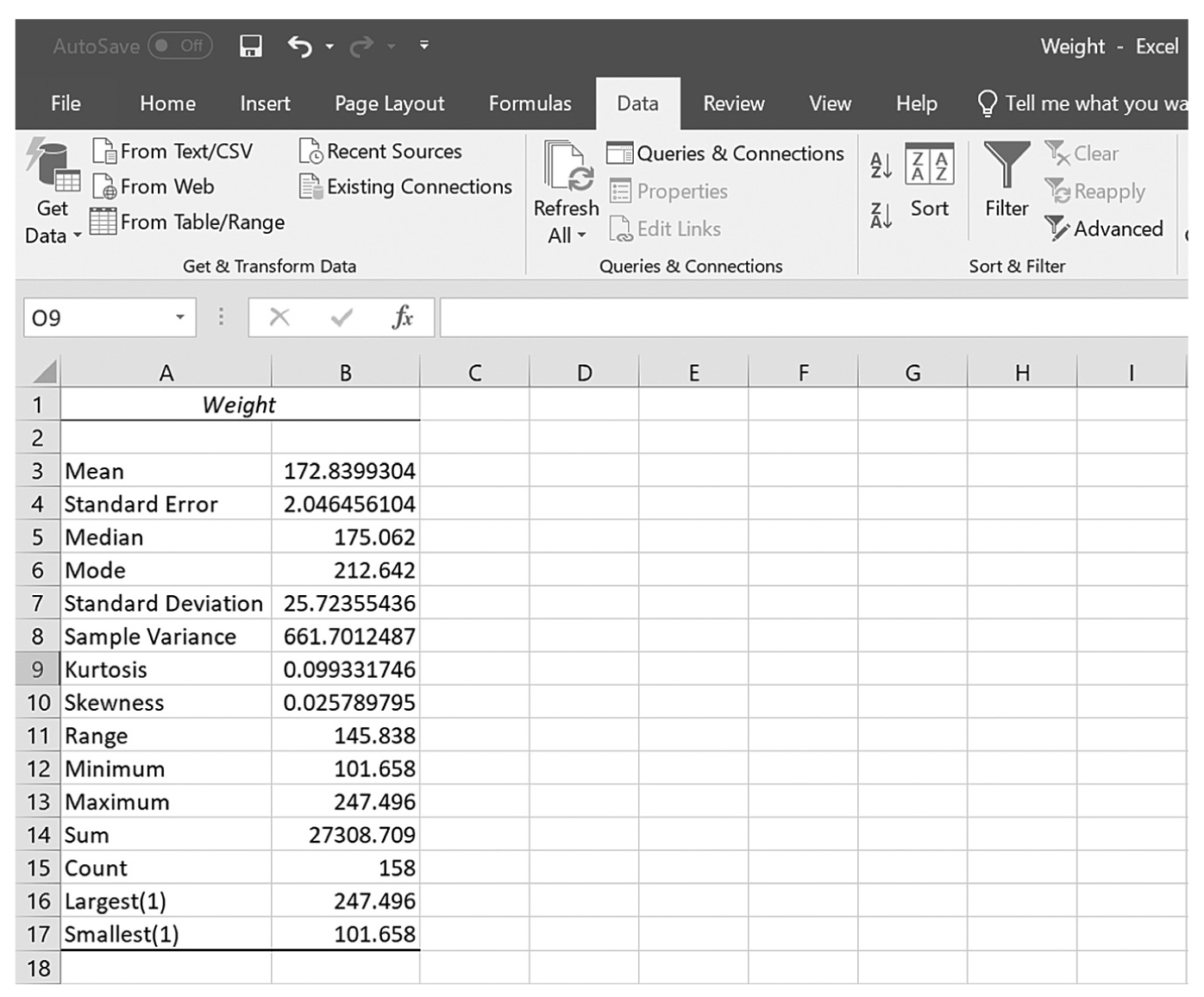
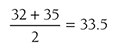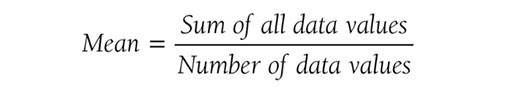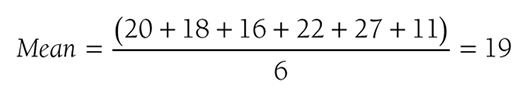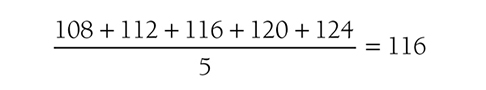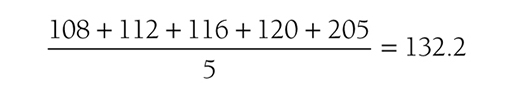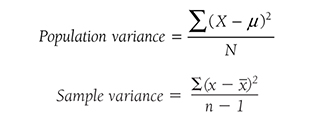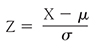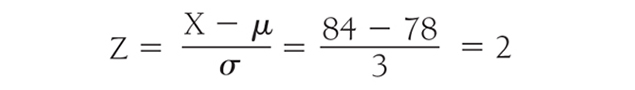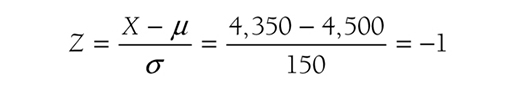Descriptive statistics help us understand whether the distribution of a continuously measured variable is normal. Figure 6-12 is an example of normal distribution of a variable, age. Some notable characteristics of normal distribution are summarized in the text that follows.

Histogram with overlying normal curve.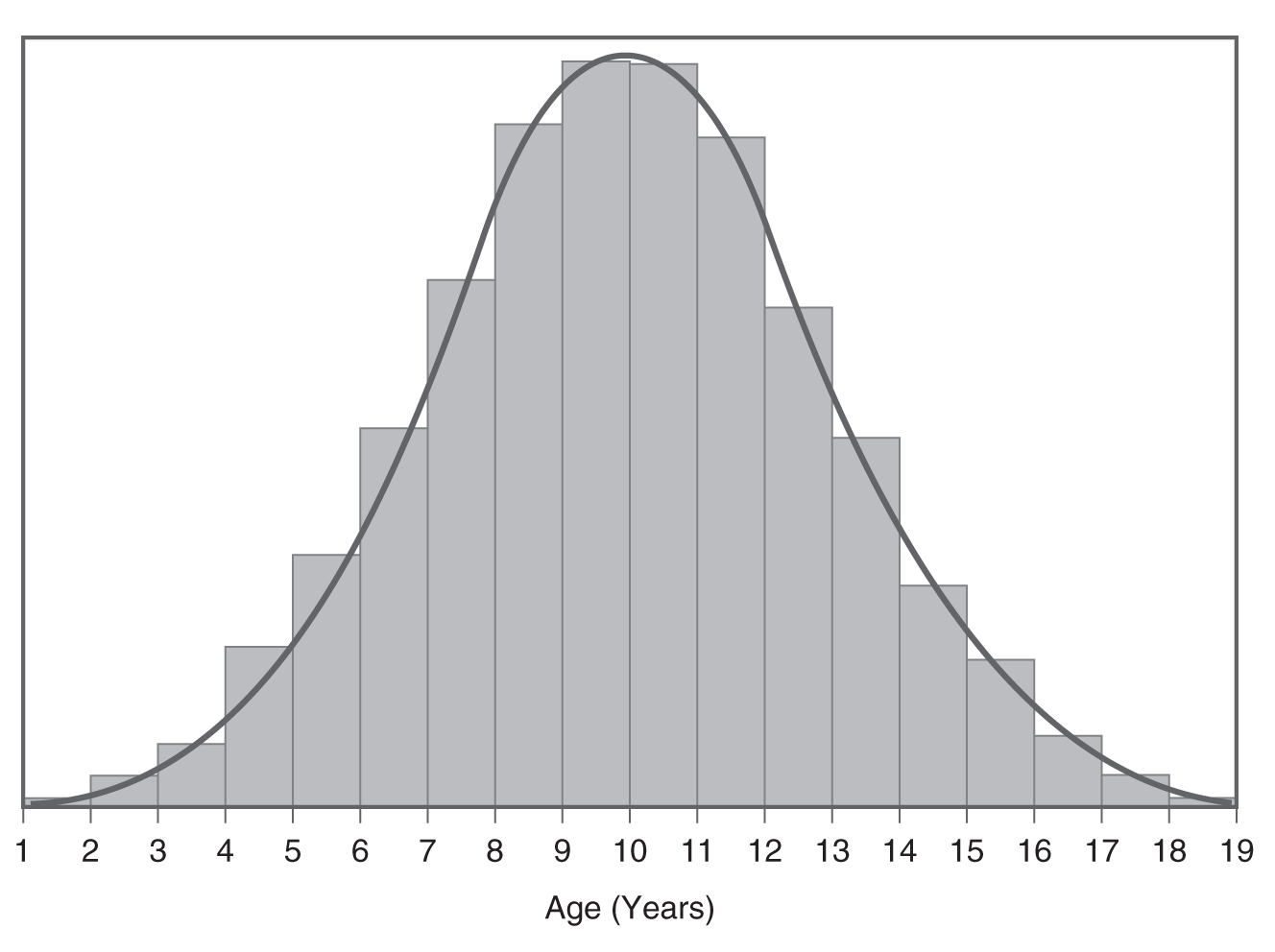

A histogram showing the age and the normal distribution are shown.

When a distribution is normal, the distribution is symmetrical and the area on both sides of the distribution from the mean is equal; in other words, 50% of the data values in the set are smaller than the mean and the other 50% are larger than the mean. In a normal distribution, the mean is located at the highest peak of the distribution, and the spread of a normal distribution can be presented in terms of the standard deviation.

Why do we care about this normal distribution so much? The most important reason is that many human characteristics fall into an approximately normal distribution, and the measurement scores are assumed to be normally distributed when conducting most statistical analyses. Therefore, if the variable is not normally distributed, the statistical results may not be trustworthy. We will discuss this more in Chapter 8.

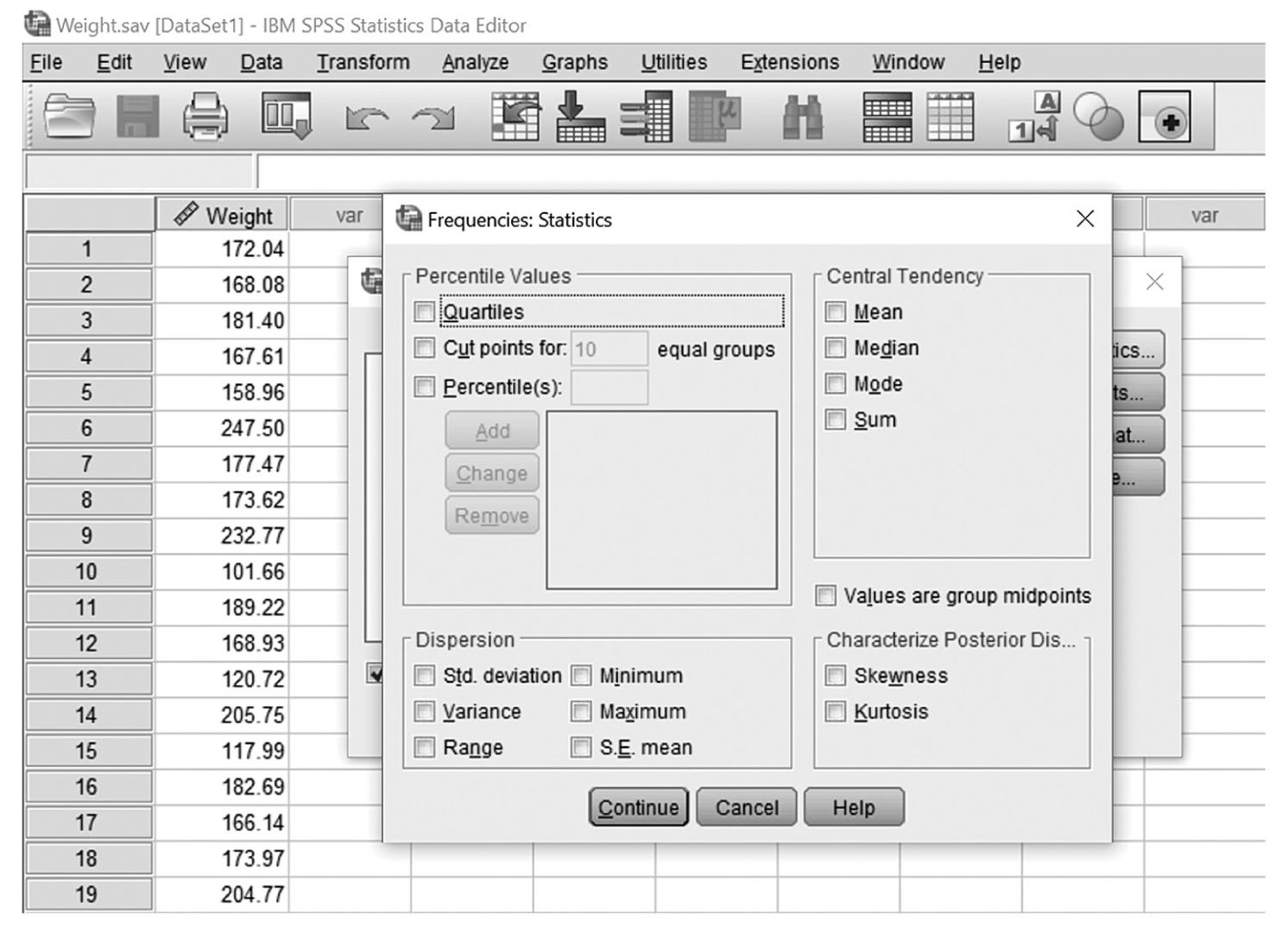
Note that no data are ever exactly/perfectly normally distributed in reality. If that is so, how do we know whether a collected data set is normally distributed? We can begin with a visual display of the data in a histogram to see if the data set is normally distributed. However, a visual check alone may not be sufficient to know whether the data are normally distributed. There are statistical measures, skewness and kurtosis, which, along with a histogram, allow us to determine whether the data set is normally distributed. Skewness is a measure of whether the set is symmetrical or off-center, which means that the probabilities on both sides of the distribution are not the same. Kurtosis is a measure of how peaked a distribution is. A distribution is said to be normal when both measures of skewness and kurtosis fall within the -1 to +1 range, and nonnormal if both measures fall either below -1 or above +1. Note that these measures can be selected in the same window as measures of central tendency and variability, which we just discussed.

Characteristics of Normal Distribution
It is bell-shaped and symmetrical.
  • The area under a normal curve is equal to 1.00 or 100%.
  • 68% of observations fall within one standard deviation from the mean in both directions.
  • 95% of observations fall within two standard deviations from the mean in both directions.
  • 99.7% of observations fall within three standard deviations from the mean in both directions.
  • Many normal distributions exist with different means and standard deviations.

Figure 6-13 shows what percentage of the data set falls within how many standard deviations away from the mean. If a variable follows a normal distribution, these rules can be applied to understand the distribution of the variable in terms of the mean and the standard deviation. In addition, different normal distributions can be found when the mean and the standard deviation are defined as shown in Figures 6-14 and 6-15.

Area under a normal distribution.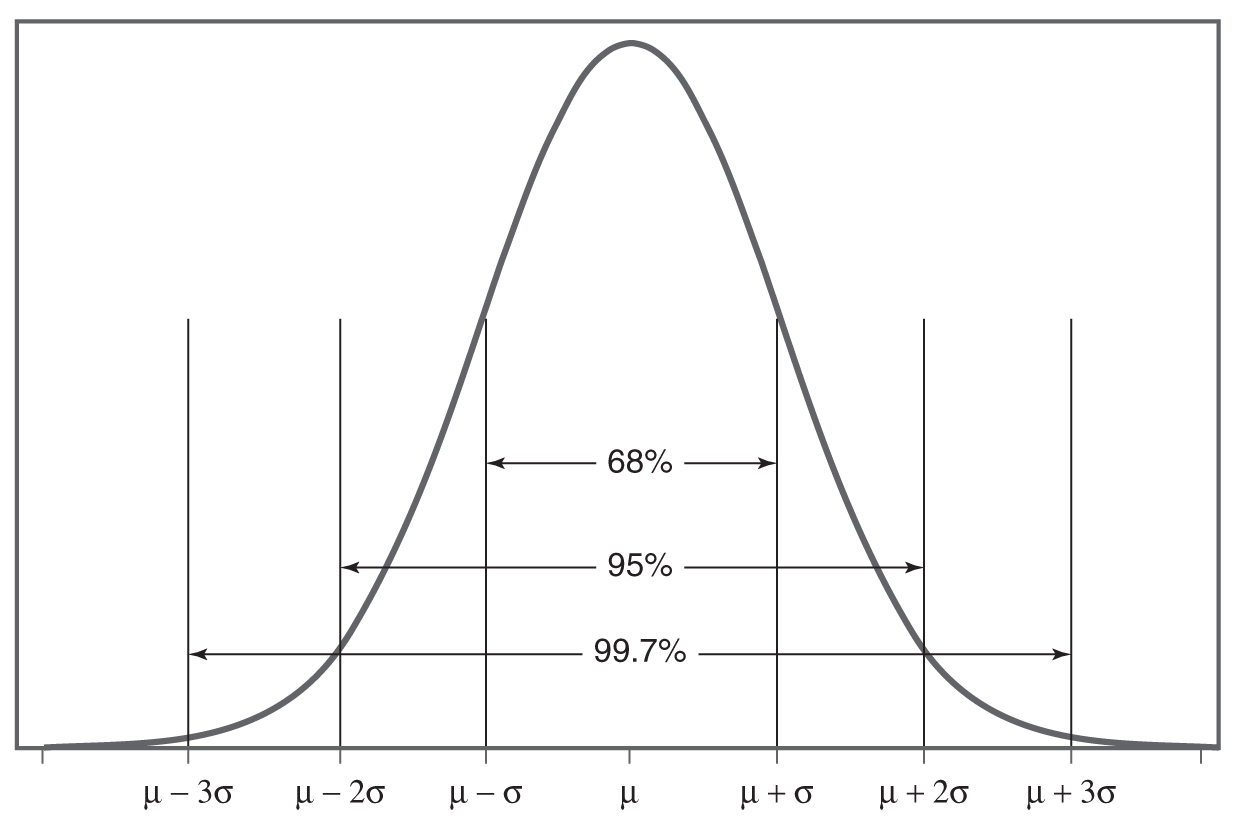

A curve shows the area under a standard normal distribution.

Normal distributions with different means.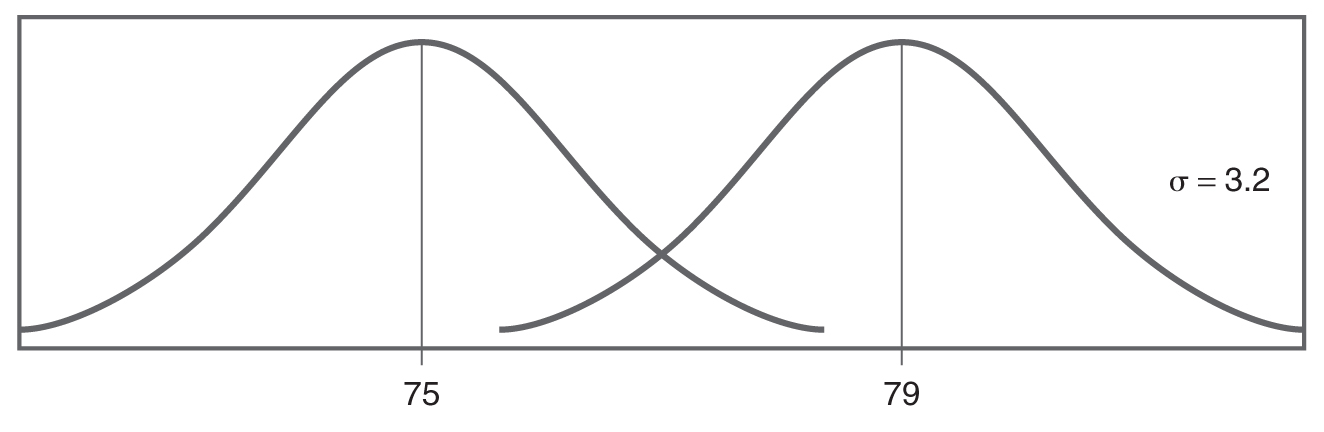

Two normal distribution curves show the mean, 75 and 79, respectively. The standard deviation equals 3.2.

Normal distributions with different standard deviations.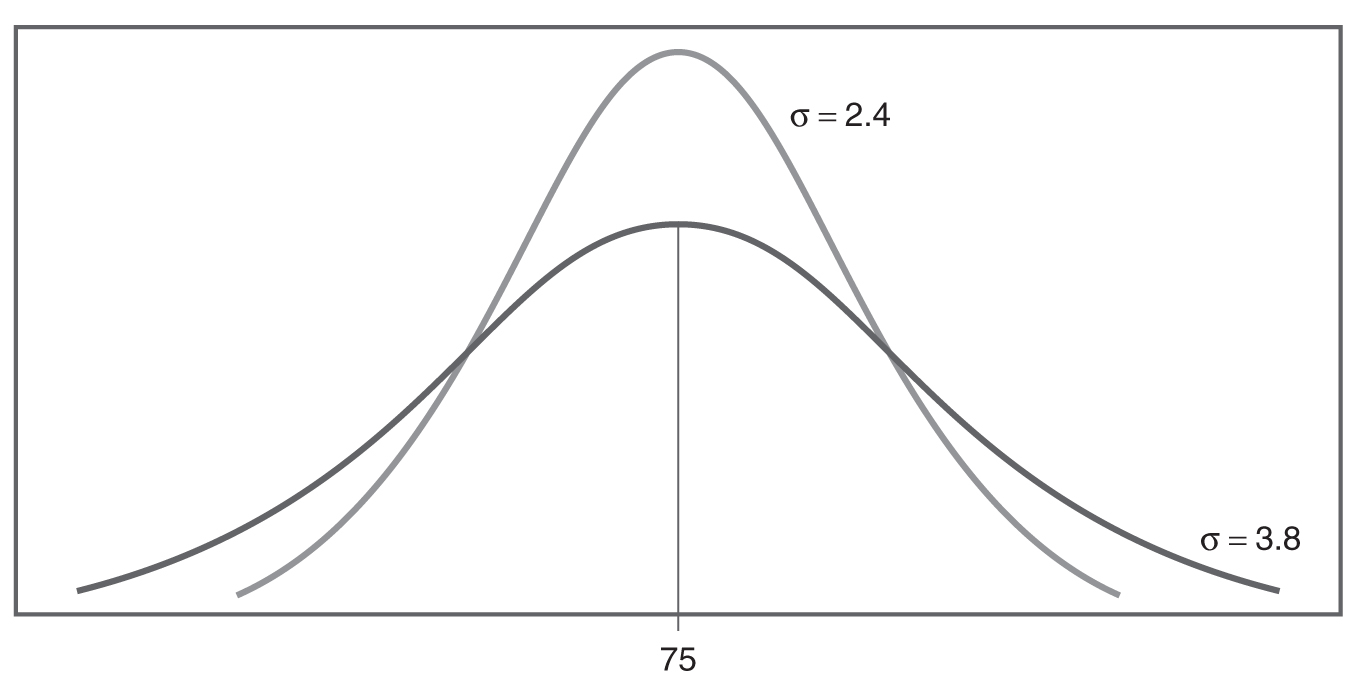

Two normal distribution curves with mean 75, show different standard deviations, 2.4 and 3.8, respectively.

We can apply the principles of the normal distribution by computing a standardized score such as a z-score. These standardized scores are useful for comparing scores computed on different scales. For example, let us consider a student who is wondering about the final exam scores in statistics and research courses. The student scored 79 out of 100 on the final exam in the statistics course and 42 out of 60 in the research course. Can the student conclude that their performance was better in statistics? Before drawing such a conclusion, the student will need to examine the distribution of scores on the two final exams. Let us assume that the final exam in statistics had a mean of 75 with a standard deviation of 3, and the final exam in research had a mean of 40 with a standard deviation of 2.5. It seems that the student did better than the average in both classes, but it is still difficult to judge in what course the student performed better. This question cannot be directly answered using different normal distributions because they have different means and standard deviations (i.e., they are not on an identical scale, which is necessary to make direct comparisons).

We need somehow to put these two different distributions on the same scale so that we can make a legitimate comparison of the student’s performance; a standard normal distribution is the solution. By definition, a standard normal distribution is one in which all scores have been put on the same scale (standardized). These standardized scores (also known as z-scores) represent how far below or above the mean a given score falls and allows us to determine percentile/probabilities associated with a given score.

Figure 6-16 shows a graphical transition from a general normal distribution to a standard normal distribution. Characteristics of the standard normal distribution are summarized in the box on the page that follows.

Transition from a general normal distribution to a standard normal distribution.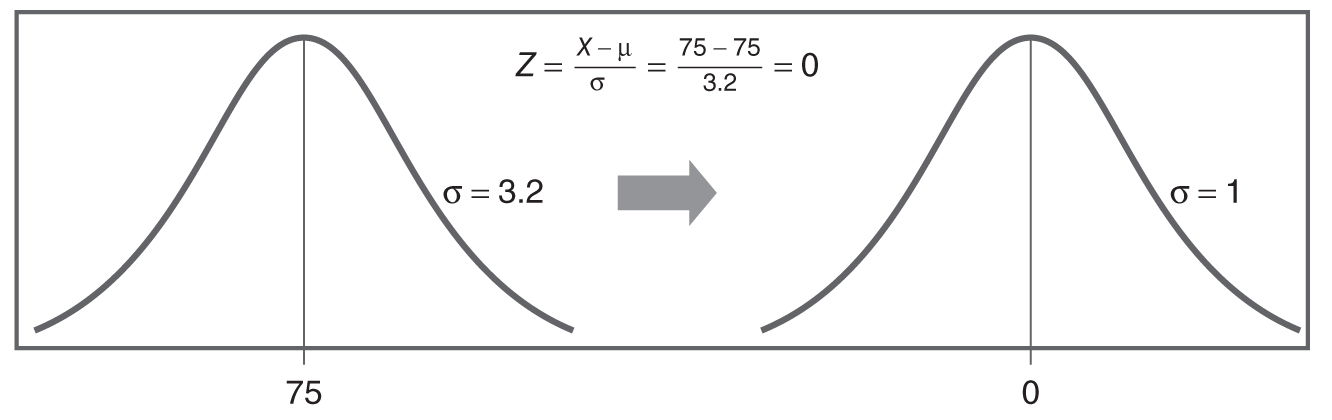

A normal distribution curve with mean 75 and standard deviation 3.2 is transitioned to a standard normal distribution curve with mean 0 and standard deviation 1. A formula reads, Z equals X minus mu, over, sigma equals 75 minus 75, over 3.2 equals 0.

To compute a z-score, you will need two pieces of information about a distribution: the mean and the standard deviation. Z-scores (standardized scores) are computed using the following equation, where the population mean (μ) is subtracted from the raw score and divided by the population standard deviation (σ). Z-scores are calculated so that positive values indicate how far a score is above the mean, and negative values indicate how far a score falls below the mean. Whether positive or negative, larger z-scores mean that scores are far away from the mean, and smaller z-scores mean that scores are close to the mean:

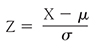
Z-scores will be positive when a student performs better than the mean on a test—the numerator of the previous equation will be positive. In contrast, z-scores will be negative when a student performs below the mean. Let us consider an example test, again a statistics final exam, with a mean of 78 and standard deviation of 3. Suppose that Brian has a final exam score of 84. His z-score will be:

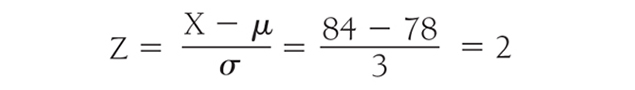
Characteristics of the Standard Normal Distribution
The standard normal distribution has a mean of 0 and a standard deviation of 1.
  • The area under the standard normal curve is equal to 1.00 or 100%.
  • Z-scores have associated probabilities, which are fixed and known.

What does Brian’s z-score of 2 mean in terms of his performance relative to the average person who took this statistics final exam? First, we can see that Brian did perform better than the average person on this final exam. Second, his z-score of 2 tells us that his score is two standard deviations above the mean of 0 (i.e, average score of 78), because a standard normal distribution has a standard deviation of 1. However, this second point about Brian’s score does not really make perfect sense to us yet. From Figure 6-17, we can see that Brian seems to have performed better than some students in his class. However, we still do not know exactly how much better he did. To find out the exact percentile rank, we need to use a z table, as shown in Figure 6-18. Steps in using the z table to find a corresponding percentile rank are summarized in the box that follows.

Brian’s z-score.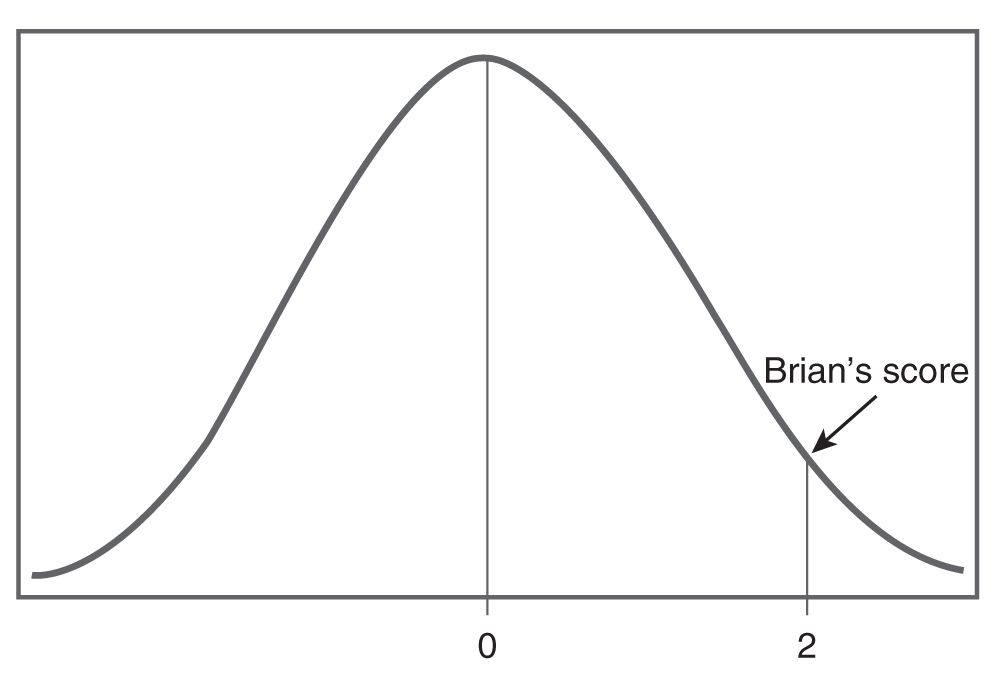

A normal distribution curve with mean 0, shows the Brian's score of 2.

z table.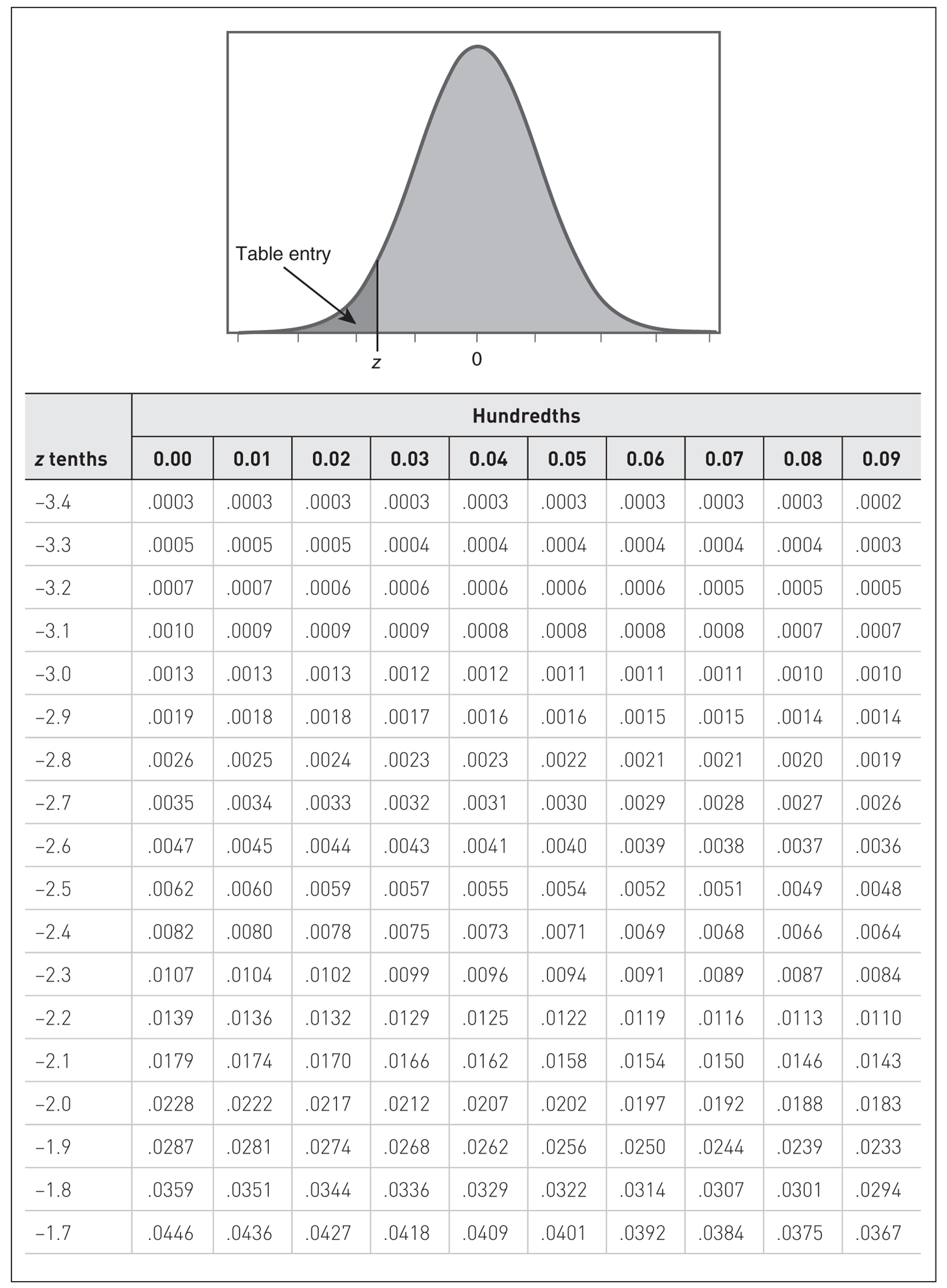

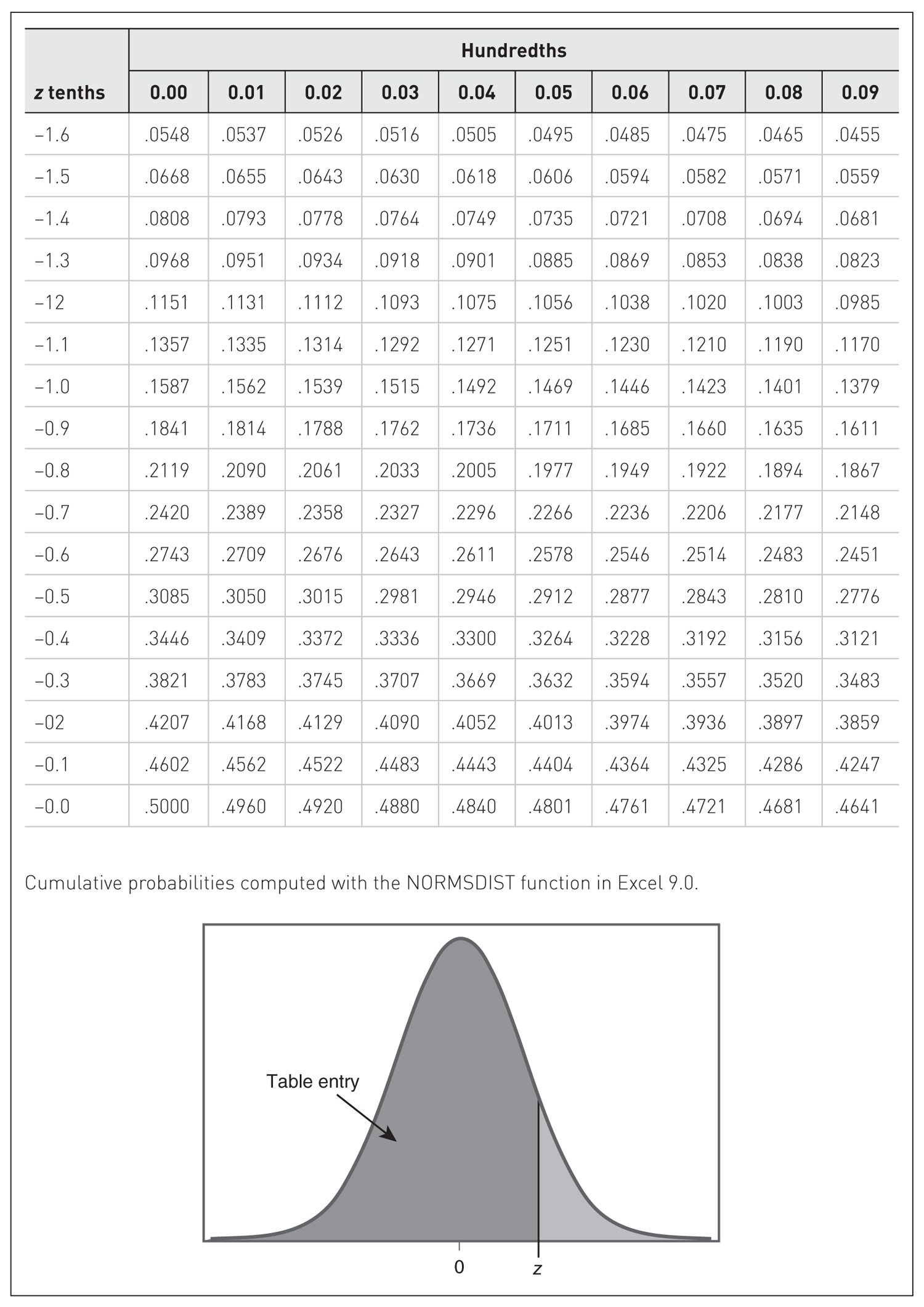
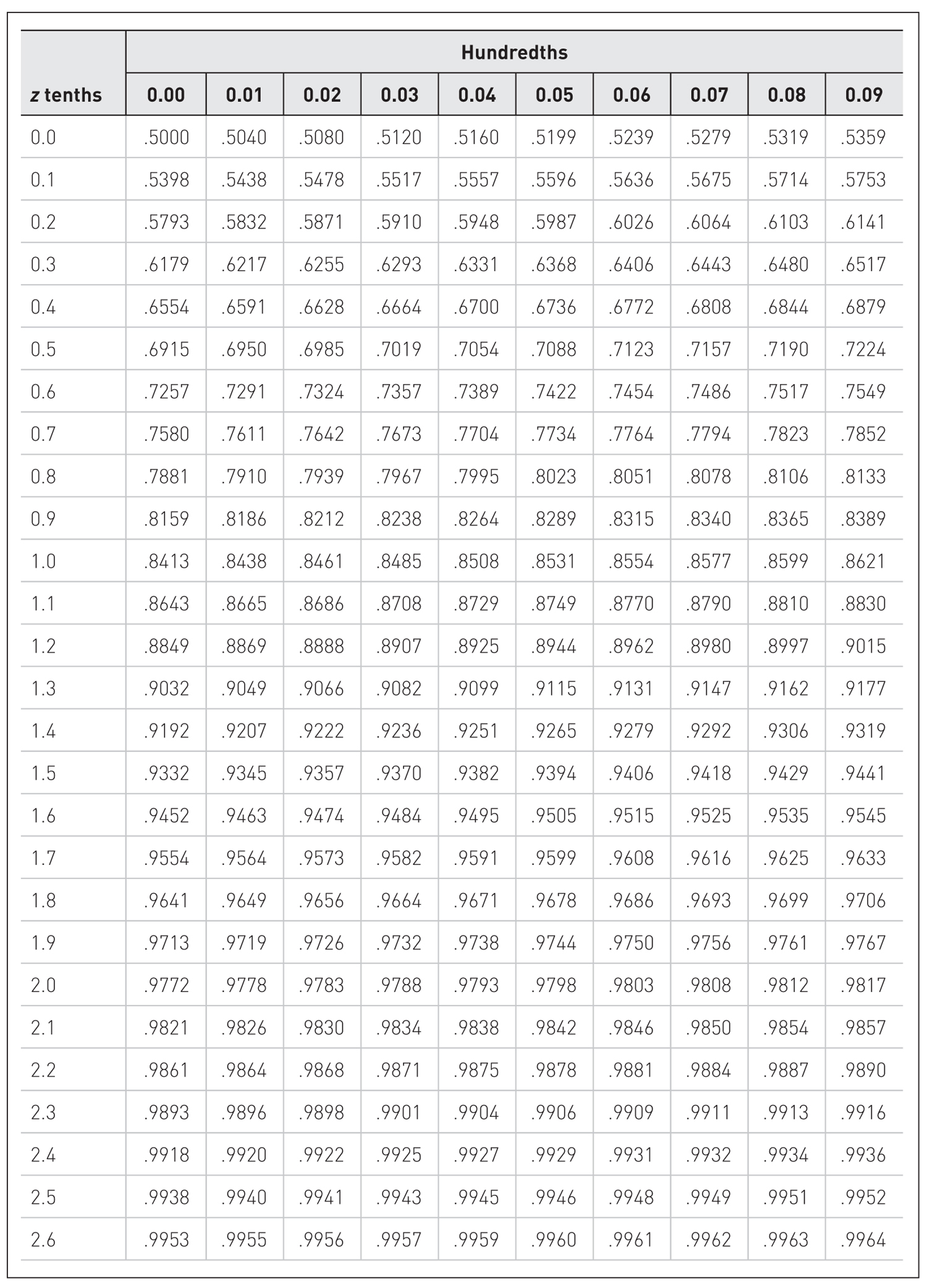
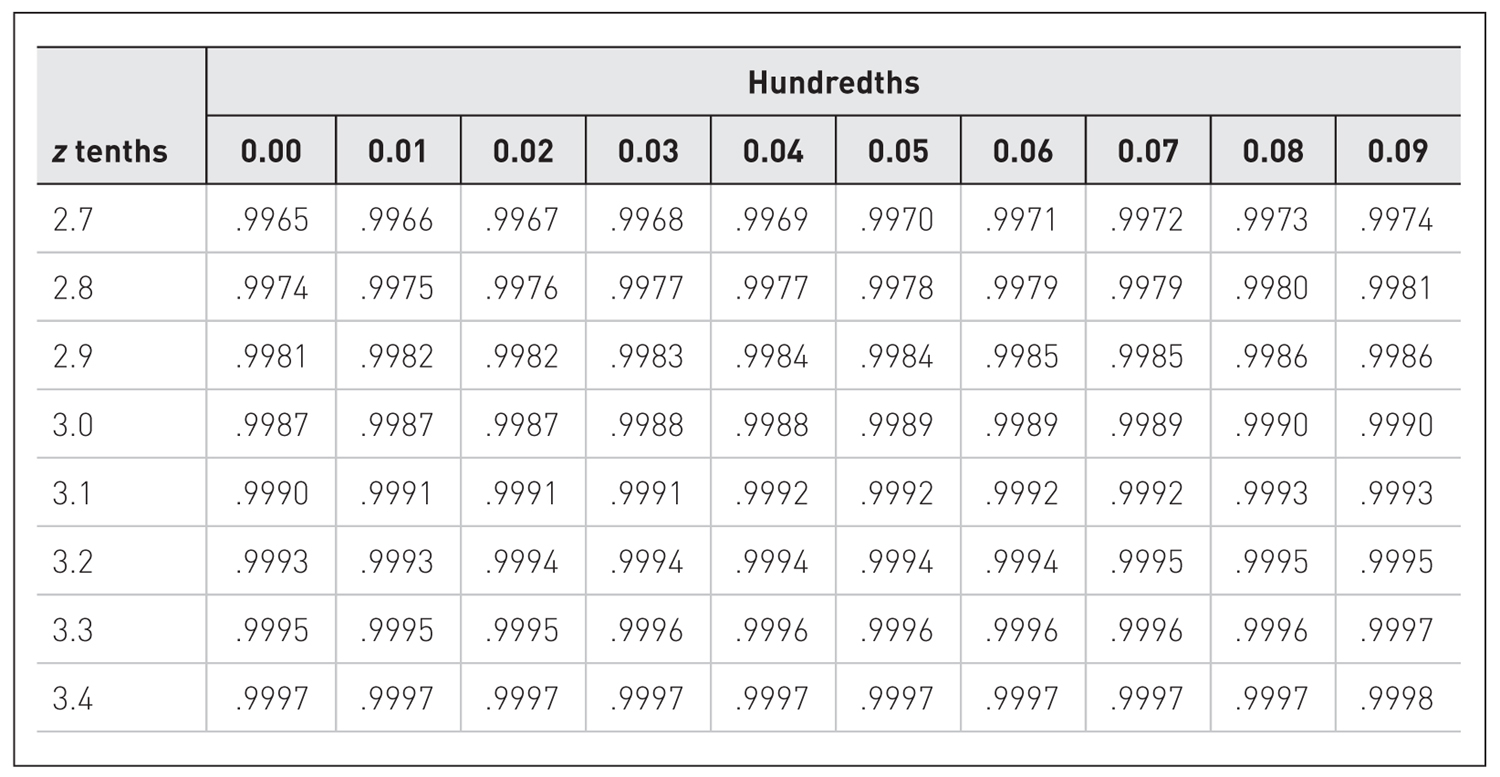
A figure shows a normal distribution curve accompanied by z table.

Using the z Table to Find a Corresponding Percentile Rank of a Score
Convert Brian’s final exam score to a corresponding z-score.
  • Locate the row in the z table for a z-score of +2.00. Note that the z-scores in the first column are shown to only the first decimal place. Also, locate the column for 0.00 so that you get 2.00 when you add 2.0 and 0.00.
  • Brian’s z-score of +2.00 gives probabilities of 0.9772 to the left.
  • Therefore, Brian’s final exam score of +2.00 corresponds to the 98th percentile. Brian did better than 98% of the students in the class.

Let us consider another example that will help us understand how to find the corresponding probability for a given score. The sodium intakes for a group of cardiac rehabilitation patients are known to have a mean of 4,500 mg/day and a standard deviation of ±150 mg/day. Assuming that the sodium intake is normally distributed, let us find the probability that a randomly selected patient will have a sodium intake level below 4,275 mg/day. First, we need to convert this value into the z-score. The corresponding z-score for 4,275 mg/day will be:

Locating the row in the z table for a z-score of -1.5 and the column for 0.00, you should get a probability of 0.0668. Therefore, the probability that a randomly selected patient will have a sodium intake below 4,275 mg/day will be 6.68%. How about the probability that a randomly selected patient will have between 4,350 mg/day and 4,725 mg/day? Notice here that we have two scores to transform. The corresponding z-score of the lower level, 4,350 mg/day, will be:

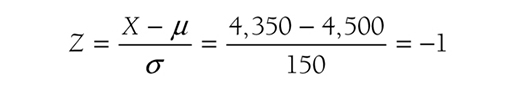
and the upper level, 4,725 mg/day, will be

Therefore, we are looking at the area under the normal curve between -1 and +1.5 standard deviations, as shown in Figure 6-19. The probability to the left of +1.5 is 0.9332, and the probability to the left of -1 is 0.1587. To get the probability between -1 and +1.5, we will subtract 0.1587 from 0.9332 and should get 0.7745. Therefore, the probability that a randomly selected patient will have a sodium intake between 4,350 mg/day and 4,725 mg/day will be 77.45%. Finding the corresponding probabilities for a given score can be tricky, so we recommend that you work on as many examples as you can, including what is provided at the end of this chapter.

The normal curve between -1 and +1.5 standard deviations.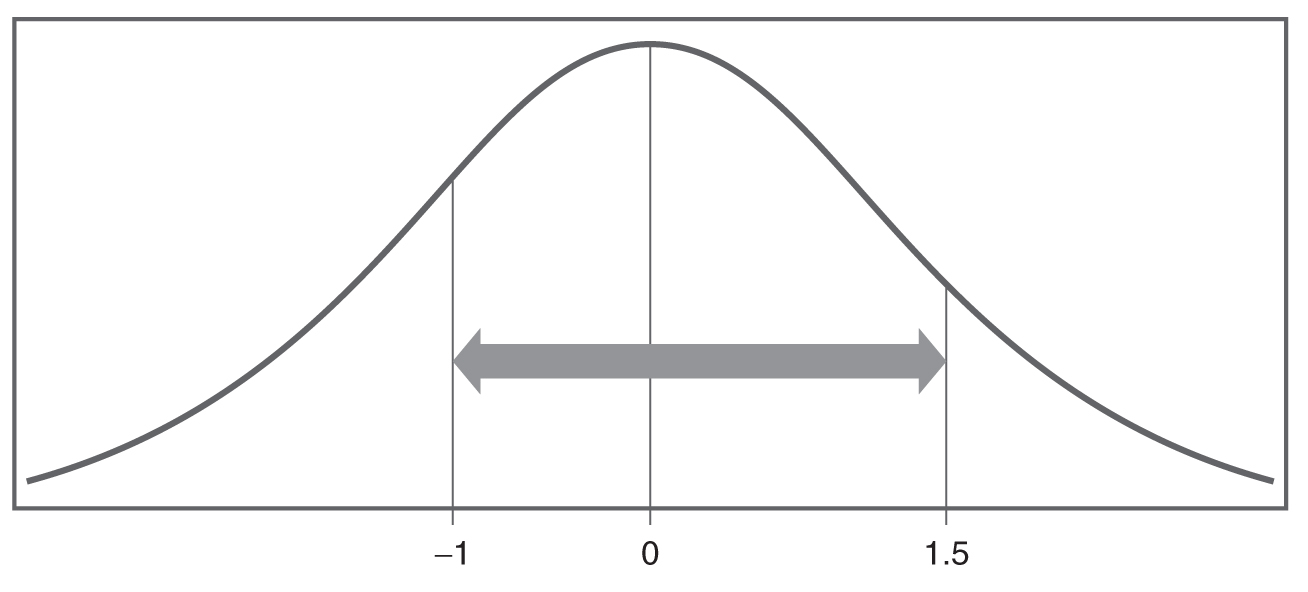

A standard normal distribution curve is shown between the standard deviations, minus 1 and plus 1.5, from the mean.

As a closing note about the standard normal distribution, recall that the following are true when a variable is normally distributed:

  • 68% of observations fall within one standard deviation from the mean in both directions.
  • 95% of observations fall within two standard deviations from the mean in both directions.
  • 99.7% of observations fall within three standard deviations from the mean in both directions.

This means that 68% of the z-scores will fall between -1 and +1, 95% of the z-scores will fall between -2 and +2, and 99.7% of the z-scores will fall between -3 and +3, because the standard normal distribution has a mean of 0 and a standard deviation of 1. This is important because any z-score that is greater than +3 or less than -3 can be treated as unusual.

Confidence Interval ⬆ ⬇

Up to this point, all of the estimates we have calculated were with a single number. Measures of both central tendency and variability were a single number, which allowed us to say that those measures were the average measurements and the spread of values on the average of a given variable, respectively. These are called point estimates. However, we may not be lucky enough to hit exactly or even close to what the actual average will be in the population, because we are likely to use a sample taken from the population. In other words, we will never be sure that our estimates will accurately reflect values in the population as a whole, as shown in Figure 6-20.

Different sample means from a population.

A diagram illustrates sampling means, with population, and four sample means, X bar, equaling 112, 115, 107, 114, and 121, respectively.

To deal with this problem, we can create boundaries, or a range of estimates, that we think the population mean will fall between, instead of computing a single estimate from a sample; these boundaries are called confidence intervals. It is another way of answering an important question, “How well does the sample statistic represent the unknown population parameter?”

Confidence intervals use confidence levels in the computation. The confidence level is determined by the researcher and reflects how accurate you want to be in computing a confidence interval as a percentage. There are three confidence levels that you can choose from: 90%, 95%, and 99% (although the 95% confidence level seems to be the most popular choice). What does confidence interval mean? Let us say that you chose a 95% confidence level to compute a confidence interval; this means that if you were to hypothetically compute 100 confidence intervals, 95 of those confidence intervals will contain the population parameter and 5 of those will not. Another way of thinking about it is to say that should we calculate 100 confidence intervals, 5 of those would likely not be accurate. There are different equations for different parameters in the computation of confidence intervals, but we will introduce only one here for a population mean and focus on how to interpret the computed confidence interval.

Let us assume that you are a nurse educator and want to investigate the average number of hours that nursing students at a local university spent per week studying for statistics. The number of hours is measured on the ratio level of measurement, and we are looking at the mean hours. Because we need to compute a confidence interval for the mean, we will use the following equation:

where

x

is the sample mean; zα/2 is the corresponding z-value for α/2, where α is equal to 1 - confidence level; s is the sample standard deviation; and n is the sample size.

Let us assume that we obtained a sample of 30 nursing students and the distribution of the number of hours that they study for statistics per week had a mean of 8 and standard deviation of 2. We want to compute a 90% confidence interval where zα/2 = 1.645. Our α is 0.10 because we are using a 90% confidence level and α/2 is 0.05. We will find that the corresponding z-score for the closest probability to 0.95 (1 - .05) inside the z table is 1.64, 1.65, or 1.645 with the (with the middle value between 1.64 and 1.65, as we cannot find the exact probability). Using 1.645, the 90% confidence interval will be:

We can conclude from this finding that 90% of the time, the mean will fall between 7.40 and 8.60 hours of studying for statistics.

Consider now that you want to compute a 95% confidence interval for the same example that we previously used. Our zα/2 is 1.96 because our α/2 is 0.025 for a 95% confidence level, and the 95% confidence interval will be:

In this case, we can conclude that 95% of the time, the mean hours of studying for statistics fall between 7.28 and 8.72.

How about a 99% confidence interval for the same example? Our zα /2 is 2.58 because our α/2 is 0.005 for a 99% confidence level, and the 99% confidence interval will be:

In this example, we can conclude that 99% of the time, the mean hours that students spend studying for statistics is between 7.06 and 8.94.

As you look at these three confidence intervals, you will notice that the confidence interval gets wider as your desired confidence level increases. This makes sense because the wider the confidence interval, the more you can be sure that the interval will include the population parameter.

Summary ⬆ ⬇

Descriptive statistics, such as measures of central tendency and variability, help us to understand typical cases in a sample and the distribution of values in a data set more clearly. Measures of central tendency include mode, median, and mean, and these provide us with an idea of what may be the typical/average data value in the data set. The mode should be used only for categorical data, as it basically counts frequency. Because the median is less sensitive to unusual data values, it should be reported when an unusual data value is present in the data set. Otherwise, the mean should be reported, as it possesses statistically preferable characteristics.

Measures of variability include the range, the interquartile range, the variance, and the standard deviation, and these convey the spread of values and give us an idea of the accuracy of the measures of central tendency. The range should be used as a crude measure of variability, as it is extremely sensitive to the presence of unusual data values. The interquartile range should be reported when an unusual or outlying data value is present in the data set. Otherwise, the standard deviation should be reported, as it possesses statistically preferable characteristics.

A normal distribution is a very important probability distribution that can represent many human characteristics, such as height, weight, and blood pressure. Skewness and kurtosis can be used to assess whether a variable is normally distributed; values should be between -1 and +1 in order to be normal. It is important that variables of interest be normally distributed, as most statistical analyses assume a normal distribution.

When a variable is normally distributed, 68% of observations will fall within one standard deviation from the mean, 95% of observations will fall within two standard deviations from the mean, and 99.7% of observations will fall within three standard deviations from the mean. Any value that falls outside of the three standard deviation range can be treated as an unusual value for the data set.

Z-scores are a good example of how we can compute standardized scores to determine where any given score falls in a normal distribution. We can use standardized scores to make comparisons of a single score, such as on a standardized test, with all other scores.

Instead of estimating an unknown population parameter with a single number or point estimate, we can compute an interval, called a confidence interval, as a different way of answering the question, “How well does the sample statistic represent an unknown population parameter?” Confidence intervals are interpreted as the interval that will include the true parameter with a given confidence level, either 90%, 95%, or 99%. As the percentage of the confidence level goes up (i.e., increased confidence that the mean falls within that range) the likelihood of confidence interval including a true population parameter increases.

Critical Thinking Questions ⬆ ⬇

  1. What is the purpose of computing descriptive statistics? Why should we include these with visual displays of a data set?
  2. Which measure of central tendency and variability should be reported when an unusual data value is present in the data set? Why?
  3. The 95% confidence interval for sodium content level in 32 nursing home patients is (4,250 mg/day, 4,750 mg/day). What does this confidence interval tell us?

Self-Quiz ⬆ ⬇

  1. True or false: Descriptive statistics are used to summarize characteristics of the sample and the measures in the data set.
  2. True or false: The variance of length of stay at a local hospital is 25. The standard deviation is 5, and this is how each value differs on average from the mean.
  3. Which of the following is not a measure of central tendency?
    1. Mode
    2. Interquartile range
    3. Mean
    4. Median
  4. Find the area under the normal distribution curve in the following locations:
    1. To the left of z = -0.59
    2. To the left of z = 2.41
    3. To the right of z = -1.32
    4. To the right of z = 0.27
    5. Between -0.87 and 0.87
    6. Between-2.99 and -1.34
  5. The average time it takes for emergency nurses to respond to an emergency call is known to be 3 minutes. Assume the variable is approximately normally distributed and the standard deviation is 1 minute. If we randomly select an emergency nurse, find the probability of the selected nurse responding to an emergency call in less than 2 minutes.
  6. Twenty-five local nursing home residents have an average age of 72, and the standard deviation is 8. The director of the nursing home wants to compute a 95% confidence interval to understand the accuracy of an estimate for the average age of all residents. What is the 95% confidence interval?
    1. (65.23, 78.77)
    2. (68.86, 75.14)
    3. (65.00, 74.00)
    4. (62.86, 82.14)

Reference ⬆

Blytt, K., Bjorvatn, B., Husebo, B., &Flo, E. (2018). Effects of pain treatment on sleep in nursing home patients with dementia and depression: A multicenter placebo-controlled randomized clinical trial. International Journal of Geriatric Psychiatry, 33, 663μ670.

Johnson, K., Razo, S., Smith, J., Cain, A., &Soper, K. (2019). Optimize patient outcomes among females undergoing gynecological surgery: A randomized controlled trial. Applied Nursing Research, 45, 39μ44.

Morin, L., Calderon Larrañaga, A., Welmer, A. K., Rizzuto, D., Wastesson, J. W., &Johnell, K. (2019). Polypharmacy and injurious falls in older adults: a nationwide nested case-control study. Clinical epidemiology, 11, 483-493. https://doi.org/10.2147/CLEP.S201614