Throughout this text, we have stressed how important a visual check of statistical findings can be. A visual check is a useful first step in understanding the existence and nature of the relationship, and a scatterplot is a good choice for creating a visual display of the correlation. This is simply a two-dimensional plot between two variables of interest, indicating how the data are spread between the variables. We refer to the relationship between two variables as a bivariate relationship (bi meaning two). Figure 9-1 is an example scatterplot showing the relationship between age and depression.
Example scatterplot between age and depression, showing a positive relationship.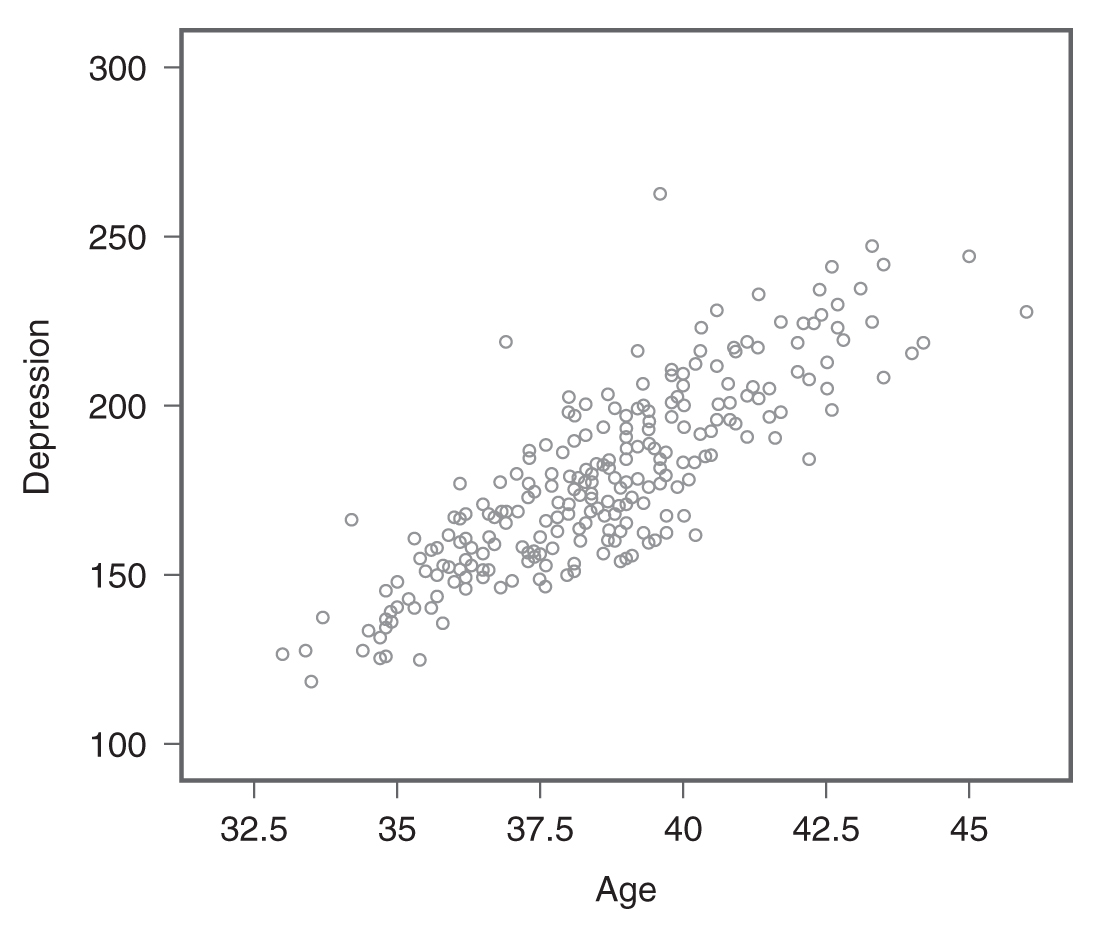
A scatterplot shows the relationship between age and depression.
When a scatterplot shows a pattern where the data points are moving in the same direction (i.e., one variable increases as the other increases), as in Figure 9-1, we say that the variables are positively related. However, the variables are said to be negatively related if the data points move in the opposite direction (i.e., one variable increases as the other decreases) as in Figure 9-2. If the variables are not related, the data points are scattered randomly (Figure 9-3).
Example scatterplot showing a negative relationship.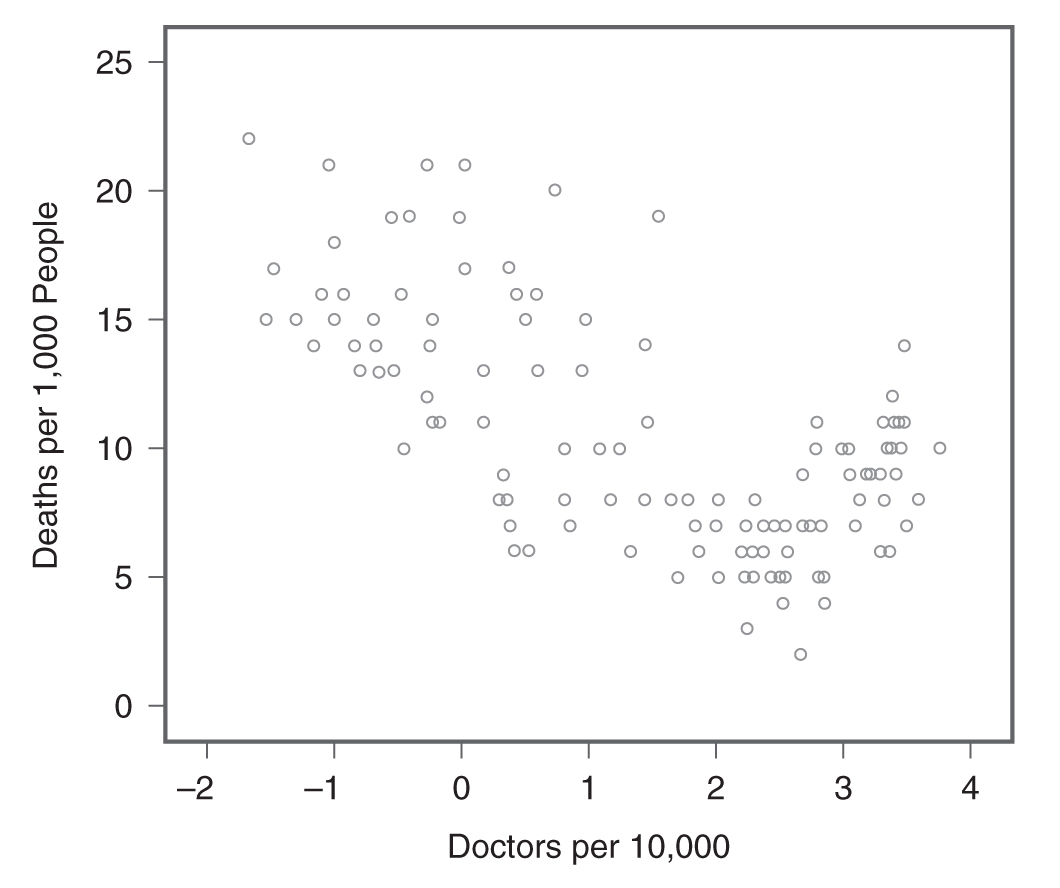
A scatterplot shows the relationship between doctors per 10,000 and deaths per 1,000 people.
Example scatterplot showing no relationship.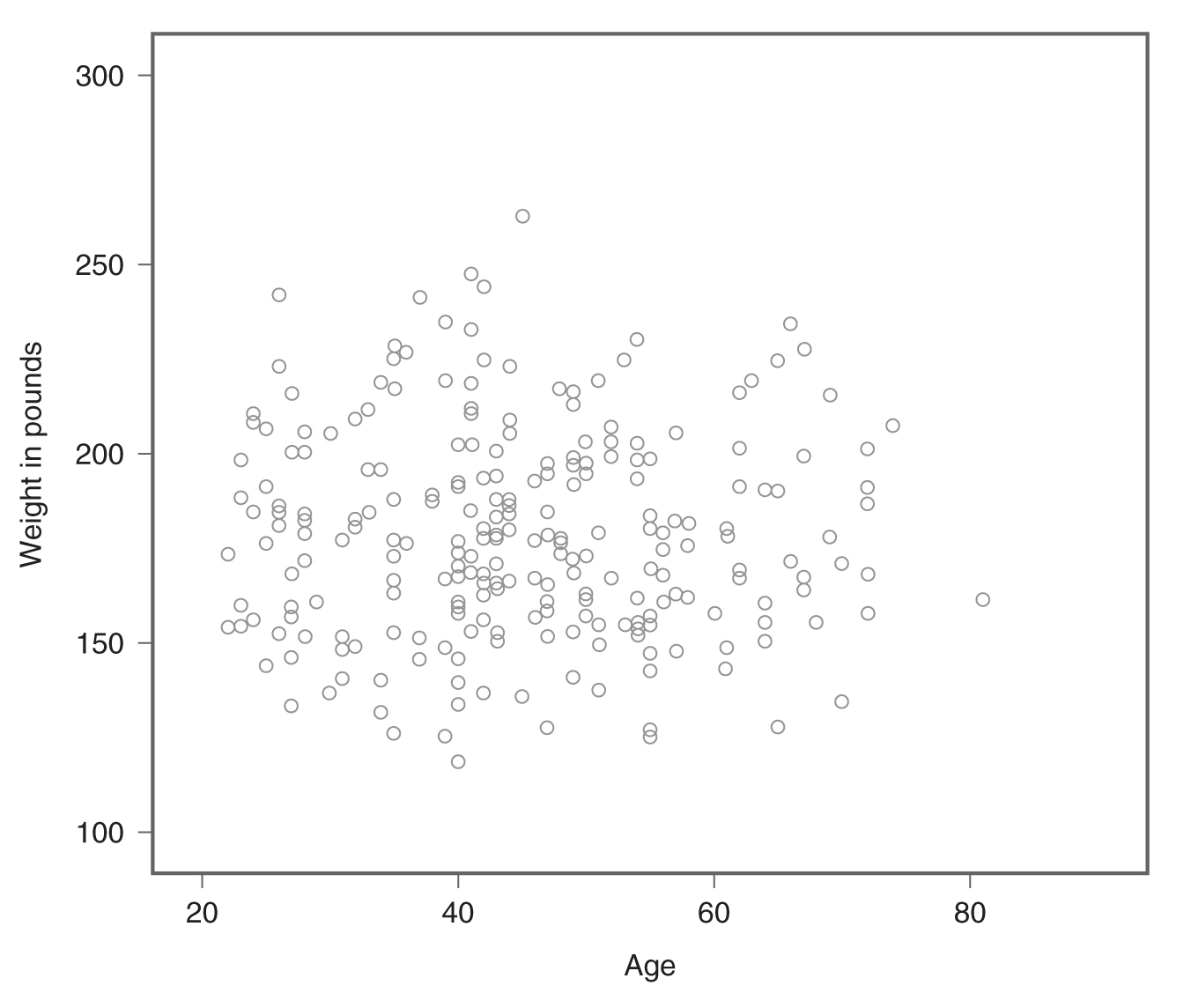
A scatterplot shows the data points scattered randomly.
Scatterplots allow us to examine the relationships between variables with visual ease, but a visual inspection can also be somewhat subjective, especially when the relationship is not strongly positive, not strongly negative, or not related. In addition, it is difficult to precisely describe the relationship and the strength of the relationship by visual inspection only. We need a numeric measurement to precisely define both the direction and strength of the relationship.
The simplest way to numerically define the relationship between variables is to determine whether the two variables covary. The measurement is called covariance and can be found using the following formula:
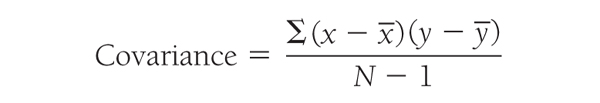
where
x
is the mean of variable x,y
is the mean of variable y, and N is the total number of observations.To explain how covariance is computed, consider the following data set:
- Number of years in employment (x): 5 2 4 3 1
- Level of job satisfaction (y): 6 9 4 7 2

First, you need to calculate the means of both variables, x and y, for each subject. You will then subtract the corresponding mean from each and every data value to calculate deviations between a data value and the mean for both variables. Finally, dividing the sum of products between deviations in x and deviations in y with nμ 1 (degrees of freedom) equals covariance.
Covariance for the previous data set turned out to be 0.75, but what does this mean? Covariance can range from negative infinity to positive infinity and tells us how the two variables of interest are related to each other. Whether a covariance is positive or negative tells us whether the relationship is positive or negative. When a covariance is zero, it means that the two variables are not related. Therefore, our example covariance of 0.75 indicates that our variables, the number of years in employment and level of job satisfaction, are positively related, yet the relationship is very weak as the covariance measure is very close to zero.
The interpretation of covariance seems relatively easy, but there is a major drawback of using covariance as a measure of relationship, in that covariance is not a standardized measure. In other words, the coefficient depends on the measurement scale, and it may not allow for comparisons between one covariance and another. Therefore, we need a standardized measure of relationship to allow us to make such a comparison, and correlation is such a measure.
Pearson’s r is a standardized measure of the relationship between two or more variables and can be found using the following formula:
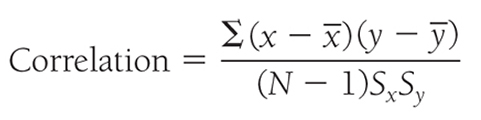
where
x
is the mean of variable x,y
is the mean of variable y, N is the total number of observation, Sx is the standard deviation of x, and Sy is the standard deviation of y. When we are dealing with a population, correlation is denoted as ρ, but it is denoted as r when we are dealing with a sample. More precisely, the coefficient in the previous equation is known as the Pearson’s correlation coefficient.As the correlation is a standardized measure of the relationship, we can make a scale-free comparison between coefficients that ranges between -1 and +1. A coefficient of -1 indicates a perfect negative relationship, meaning that a variable goes down with exactly the same unit change as the other variable goes up, and a coefficient of +1 indicates a perfect positive relationship, meaning that a variable goes up as well with exactly the same unit change as the other variable goes up. A coefficient of 0 indicates no relationship between the two variables.
When interpreting a correlation coefficient, a general rule, as shown in Box 9-1, can be applied. However, the correlation coefficient should always be interpreted along with the corresponding p-value because the interpretation can be sample specific. Both Excel and IBM SPSS Statistics software (SPSS) will perform a t-test on a correlation coefficient to see if we have strong evidence for the null hypothesis, or whether the correlation coefficient is zero is true or not.
Interpreting a correlation coefficientCorrelation:
|
To compute the Pearson correlation coefficient in Excel, you will use correlation.xlsx and can use the CORREL function or the Analysis ToolPak add-in that we discussed in Chapter 6. In order to use the CORREL function, you can manually type “=CORREL(A2:A90,B2:B90)” in an empty cell, as shown in Figure 9-4, and press Enter to get a correlation coefficient of 0.69. Note that you can also find the CORREL function in Formula > Insert Function, as shown in Figure 9-5, and define the range of Year and Satisfaction, as shown in Figure 9-6, in order to get the same correlation coefficient of 0.69. Note, you will have to use further functions in order to get the corresponding p-value for the computed correlation coefficient. First, you will derive the t statistic from the correlation coefficient using “=(r*sqrt(n-2))/sqrt(1-r^2),” where n is the sample size, so it will be “=(0.69*sqrt(89-2))/sqrt(1-0.69^2)” for our example, which will give 8.89, as shown in Figure 9-7. Now, you will use the TDIST function with “=t.dist.2t(t, n-2)” in order to compute the p-value associated with this value so it will be “=t.dist.2t(8.89, 89-2)” for our example, which will give a very small value of 7.54468E-14 (i.e., 0.000), as shown in Figure 9-8.
Typing in the CORREL function in Excel.
An Excel screenshot shows the Correl function typed, starting with an equal sign, in the cell D 3.
Courtesy of Microsoft Excel © Microsoft 2020.
Selecting the CORREL function from the function list in Excel.
A screenshot of an Excel worksheet shows the Correl function entered in a dialog box, with heading Insert function.
Courtesy of Microsoft Excel © Microsoft 2020.
Defining the data range for the CORREL function in Excel.
An Excel screenshot shows the dialog box in which the numerical data range for the Correl function is defined.
Courtesy of Microsoft Excel © Microsoft 2020.
Computing the t statistic from the computed correlation coefficient in Excel.
An Excel screenshot shows the derivation of the t statistic from the correlation coefficient.
Courtesy of Microsoft Excel © Microsoft 2020.
Computing the p-value using the TDIST function in Excel.
An Excel screenshot shows the derivation of the p-value using the T DIST function.
Courtesy of Microsoft Excel © Microsoft 2020.
To use the Analysis ToolPak add-in, you will go to Data > Data Analysis, as shown in Figure 9-9. In the Data Analysis window, choose Correlation and then click OK (Figure 9-10). On the next window, provide the data range A2:B90 as the Input Range and E3 as the Output Range, and then click OK (Figure 9-11). This should produce the same correlation coefficient of 0.69, as shown in Figure 9-12. Note you can obtain the corresponding p-value as previously shown.
Finding Data Analysis in Excel.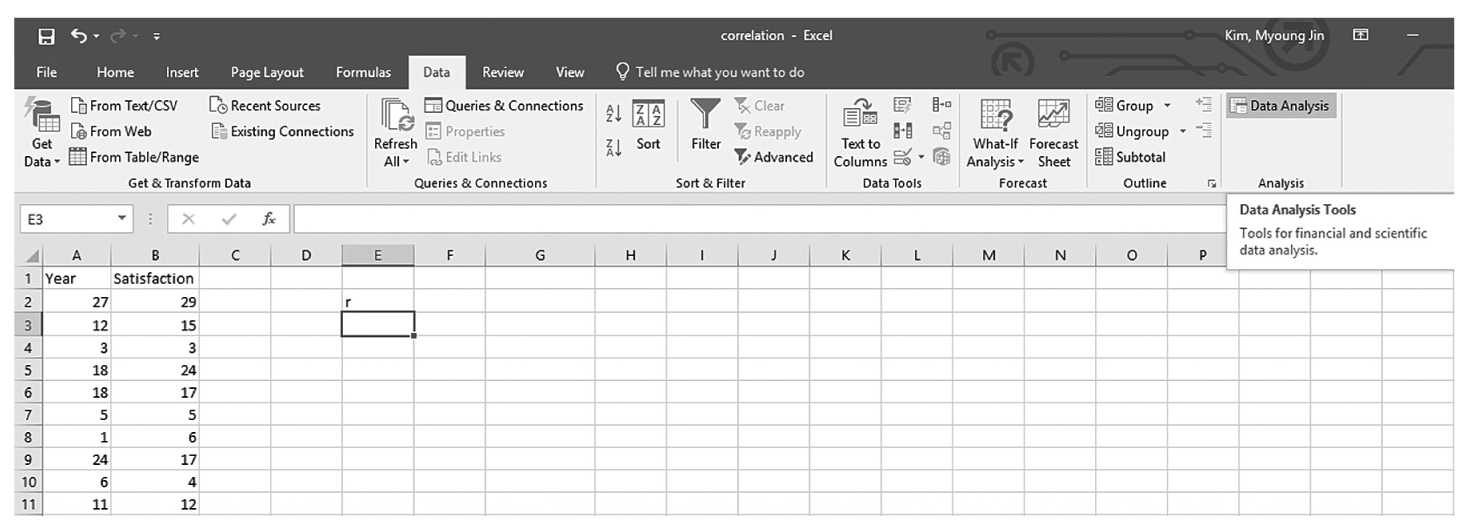
An Excel screenshot shows the Data Analysis ToolPak add-in, in the Analysis group under Data menu. Row 1 in Column A displays the heading, Year, and that in Column B the heading, Satisfaction, with numerical data displayed from row 2 through row 13.
Courtesy of Microsoft Excel © Microsoft 2020.
Selecting Correlation in the Data Analysis dialogue box in Excel.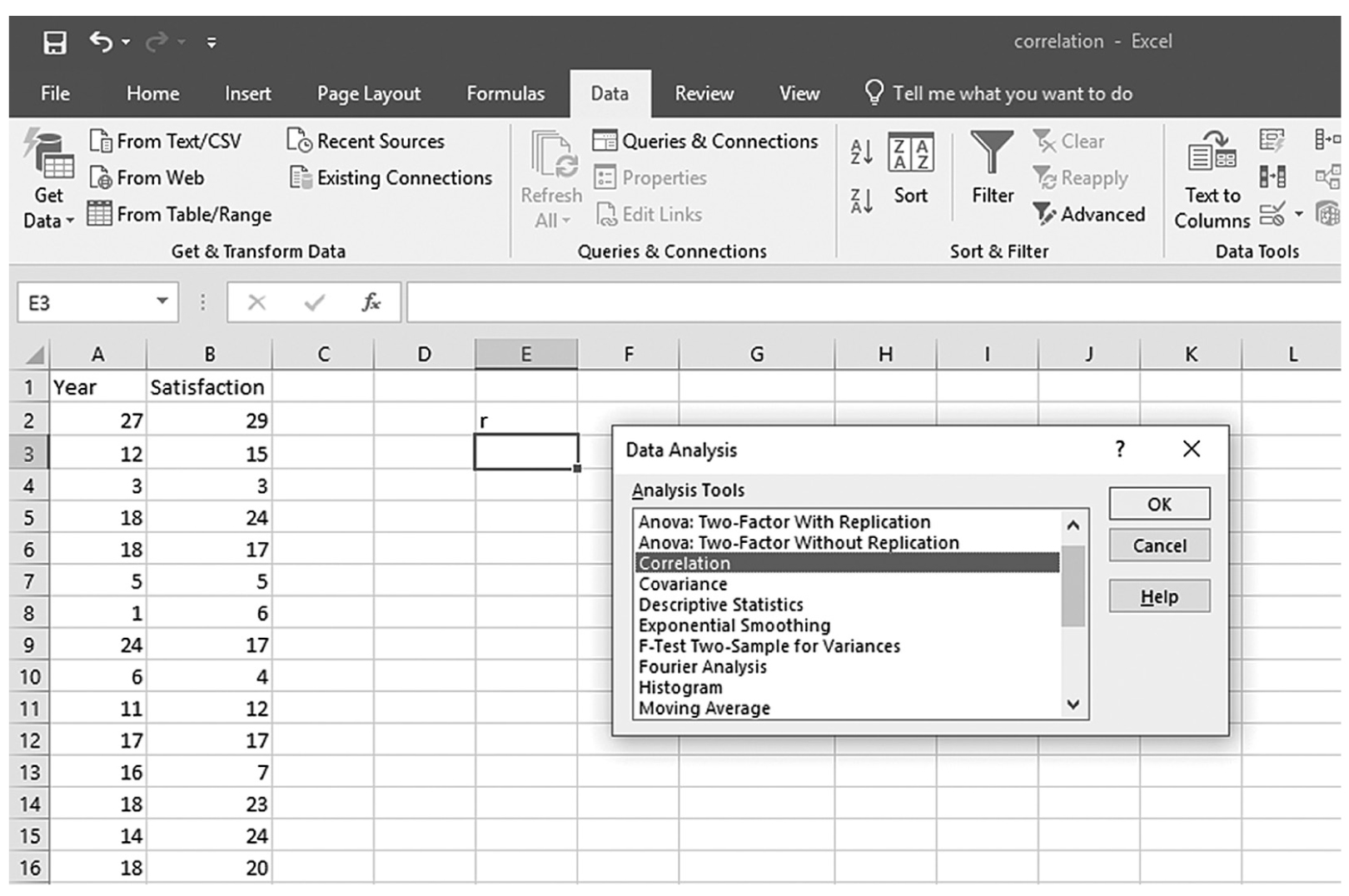
An Excel screenshot shows selection of the analysis tool, Correlation, from a list of tools in the data analysis dialog box. Row 1 in Column A displays the heading Year, and that in Column B, Satisfaction, with numerical data from rows 2 through 13.
Courtesy of Microsoft Excel © Microsoft 2020.
Defining the data range in the Correlation dialogue box in Excel.
An Excel screenshot shows the Correlation dialog box with fields to define data. The data in the worksheet has the column headings, Year and Satisfaction, with a list of numerical data.
Courtesy of Microsoft Excel © Microsoft 2020.
Output for correlation coefficient in Excel.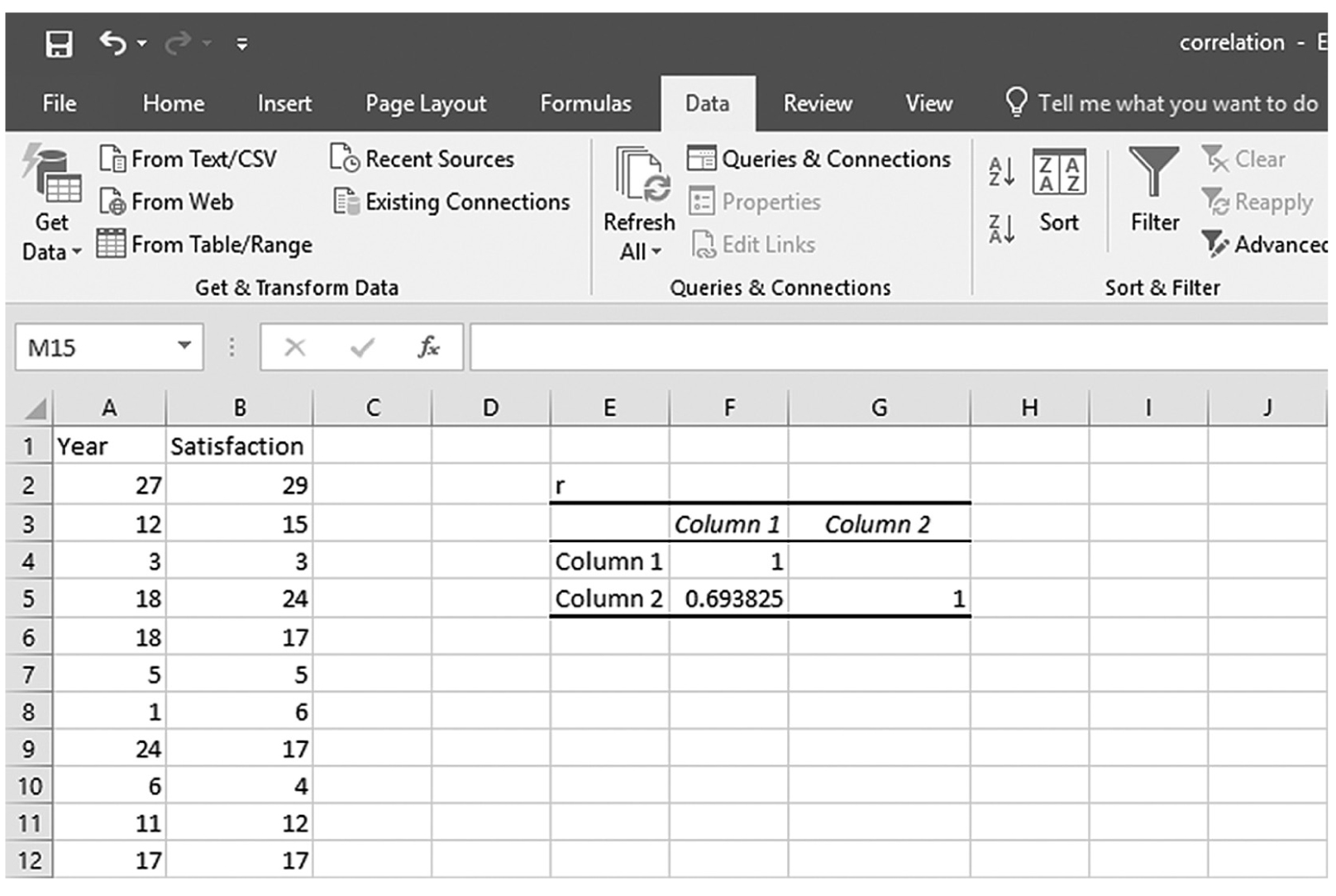
An Excel screenshot shows the output for correlation coefficient. The data in the worksheet has the column headings, Year and Satisfaction, with a list of numerical data, in Columns A and B.
Courtesy of Microsoft Excel © Microsoft 2020.
To compute the Pearson correlation coefficient in SPSS, you will use correlation.sav and go to Analyze > Correlates > Bivariates, as shown in Figure 9-13. In the Bivariate Correlations dialogue box, you will select the variables that you are interested in investigating a relationship between and move them over to the right window by clicking the arrow button in the middle, as shown in Figure 9-14. Pearson’s coefficient is checked by default in this dialogue box, so you should leave it unless parametric assumptions are violated. Clicking “OK” will then produce the output of requested correlation coefficients. An example output is shown in Table 9-1.
Selecting correlation in SPSS.
A screenshot in S P S S shows the selection of the Analyze menu, with Correlates command chosen, from which the Bivariates option is selected. The data in the worksheet has two columns of data, Year and Satisfaction, with a list of numerical data.
Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. “IBM SPSS Statistics software (“SPSS”)”. IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.
Defining the variables to compute correlation coefficients in SPSS.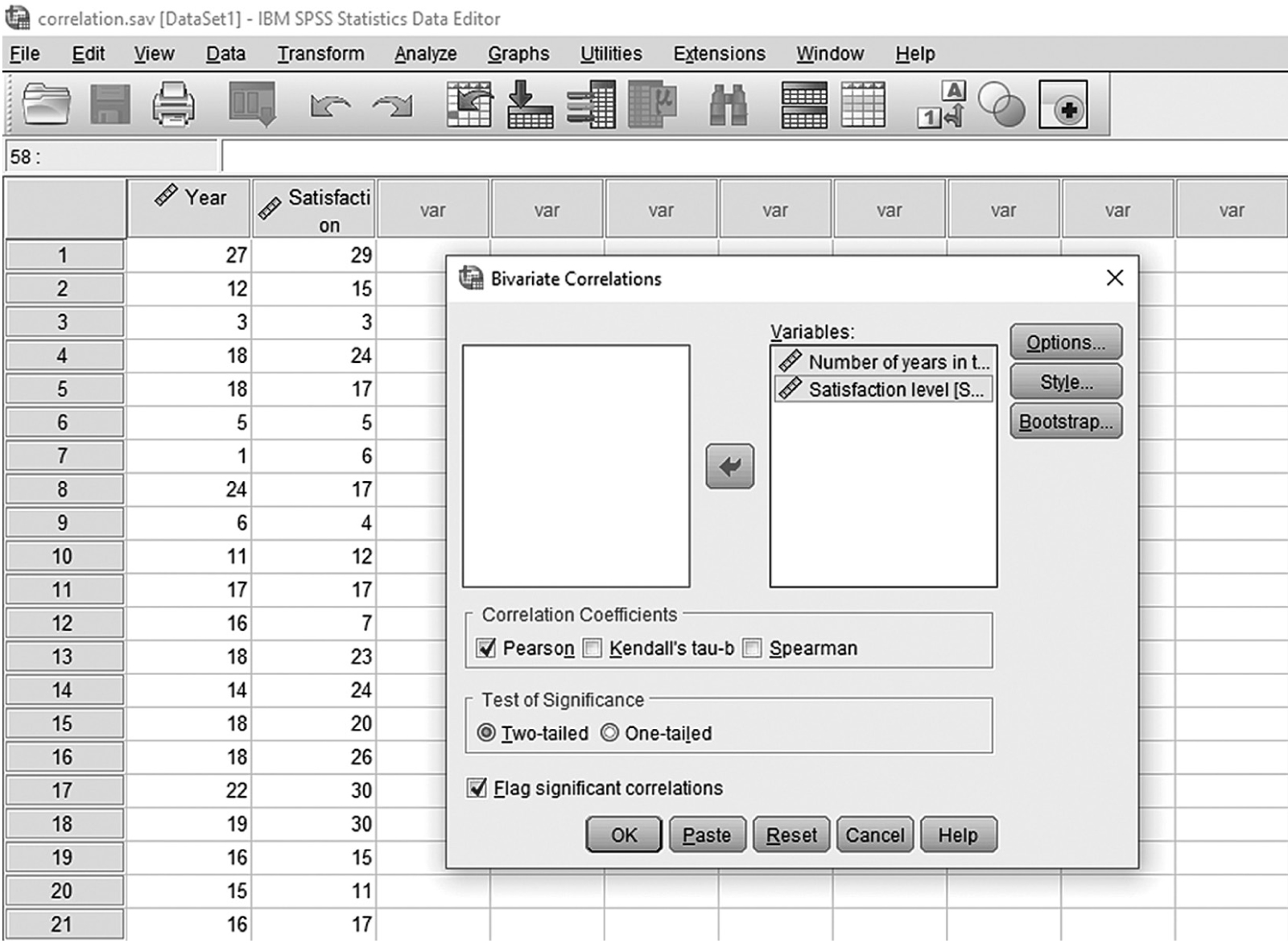
A screenshot in I B M, S P S S, Statistics Editor shows the bivariate correlations dialog box. The data in the worksheet lists numerical data under the headings, Year and Satisfaction.
Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. “IBM SPSS Statistics software (“SPSS”)”. IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.
Correlations | |||
|---|---|---|---|
Number of Years in the Current Job | Satisfaction Level | ||
Number of years in the current job | Pearson correlation | 1 | .694** |
Sig. (two-tailed) | .000 | ||
N | 89 | 89 | |
Satisfaction level | Pearson correlation | .694** | 1 |
Sig. (two-tailed) | .000 | ||
N | 89 | 89 | |
The Pearson correlation coefficient between the number of years in the current job and the level of satisfaction is .694; this indicates that there is a positive relationship between the two variables: the level of satisfaction goes up as the number of years in the current job increases. Note that the corresponding p-value of .000 in the table is small enough to rule out an association by chance between the number of years in the current job and the level of satisfaction.
Recall that we cautioned earlier that correlation does not imply causation and the direction of the influence is not always clear. Is it that job satisfaction is influenced by years on the job, or do people lengthen their time of employment because they are satisfied? Relationships may be bidirectional, or move in both directions, and correlation does not tell us what that direction is. Another important thing to note about the correlation coefficient is that the ratio of differences between and/or among correlation coefficients cannot be expressed. For example, a correlation coefficient of .50 does not mean that the relationship is twice as strong as a correlation coefficient of .25.
A correlation coefficient can be squared to provide additional information. A squared correlation coefficient is called a coefficient of determination and tells us how much variation in one variable is explained or shared by the other variable. For example, perhaps we are interested in the relationship between the number of nursing staff at a nursing home and the quality of nursing care. Let us suppose that we found a correlation coefficient between the two variables of .39. Taking a square of this correlation coefficient, we get (.39)2 = 0.1521; this means that 15.21% of the variability in quality of nursing care is explained or shared by the number of staff at a nursing home. More important, this also means that the remaining 84.79% of variability in quality of care is attributed to something other than the number of staff. The coefficient of determination can be useful in determining how important the relationship between the variables is; the larger the coefficient, the more the variables explain each other. Note that a coefficient of determination ranges between 0 and 1 as it is obtained by squaring a correlation coefficient.
Pearson’s correlation coefficient is a parametric correlation coefficient, which means that it requires parametric assumptions such as the normality assumption. When parametric assumptions are not met (such as nonnormally distributed variables or ordinal level of measurement for variables), Pearson’s correlation coefficient cannot be used to examine the relationship between the variables. Two alternatives to Pearson’s correlation coefficient in this situation are Spearman’s rho and Kendall’s tau. Both coefficients are calculated by first ranking the data and then applying the same equation we used for Pearson’s correlation coefficient. We will not discuss the detailed computation of these two statistics, but the interpretation of coefficients is done in the same manner as before. As it is not easy to obtain Kendall’s tau in Excel, we will only discuss how to obtain Spearman’s rho.
To compute Spearman’s rho in Excel, you will use correlation.xlsx and first determine the rank for each value in both year and satisfaction. With cell names of “Rank Year” and “Rank Satisfaction” given in cell C1 and D1, respectively, you will type “=RANK.AVG(A2,A$2:A$90,1)” in cell C2, as shown in Figure 9-15. With C2 selected, press and hold the Ctrl key and place the cursor on the little square on the bottom right of the cell until it changes to “+”. Clicking on the little square and dragging it down to cell C90 will rank the values of Year (Figure 9-16). You will do the same for Satisfaction in column D in order to get the ranked values for satisfaction. Type “=RANK.AVG(B2,B$2:B$90,1)” in cell D2. While pressing and holding the Ctrl key, click the cursor on the little square on the right bottom of the cell until it changes to “+” and drag it down to cell C90 in order to get the rank values of Year. Now, type “=CORREL(C2:C90,D2:D90)” in cell F2, and you should get a correlation coefficient of 0.83 (Figure 9-17).
Typing in a function to convert raw data into rank values in EXCEL.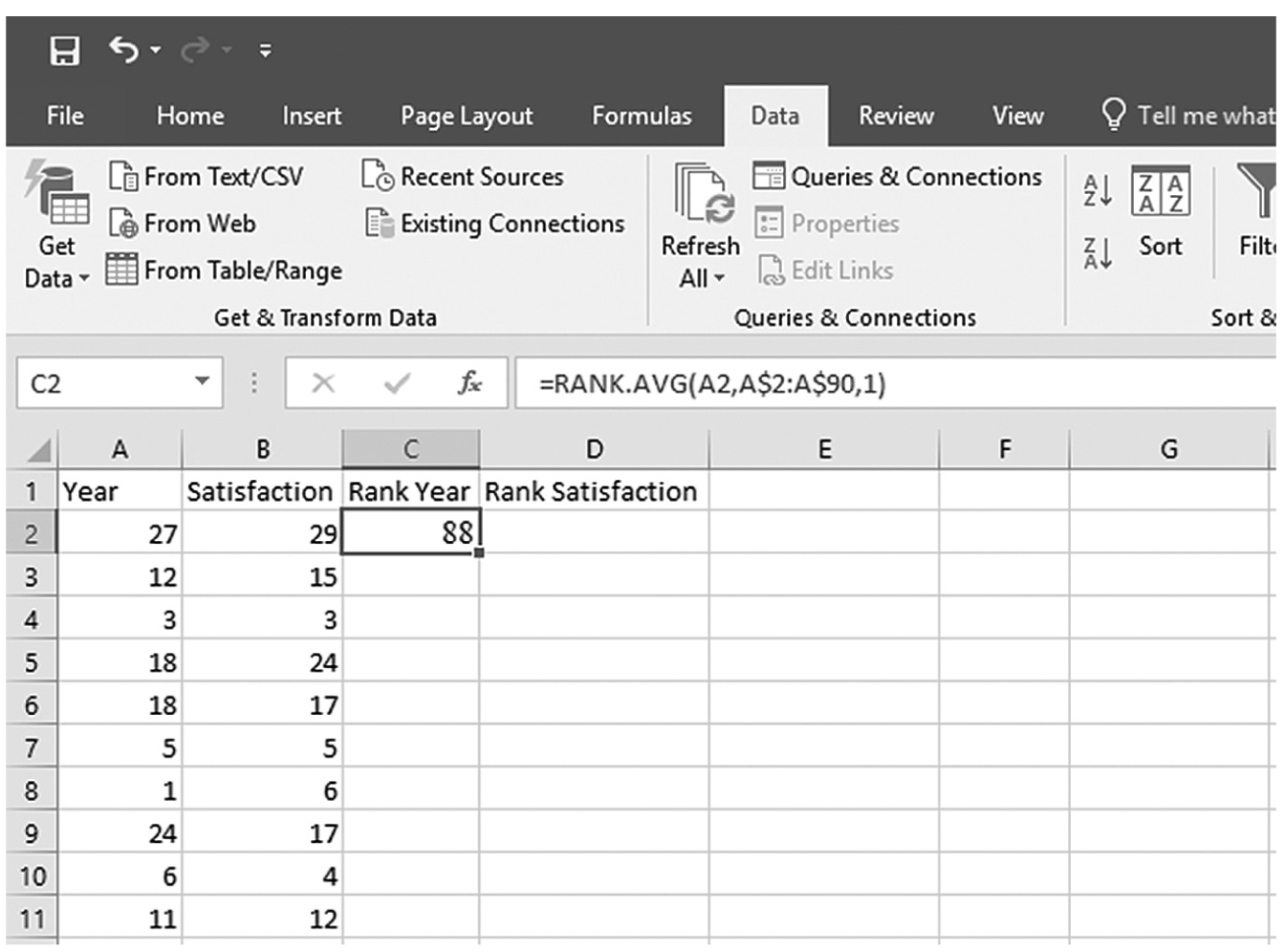
An Excel screenshot shows the entering of a function in one cell to convert raw data into rank values.
Courtesy of Microsoft Excel © Microsoft 2020.
Converting raw data into rank values in Excel.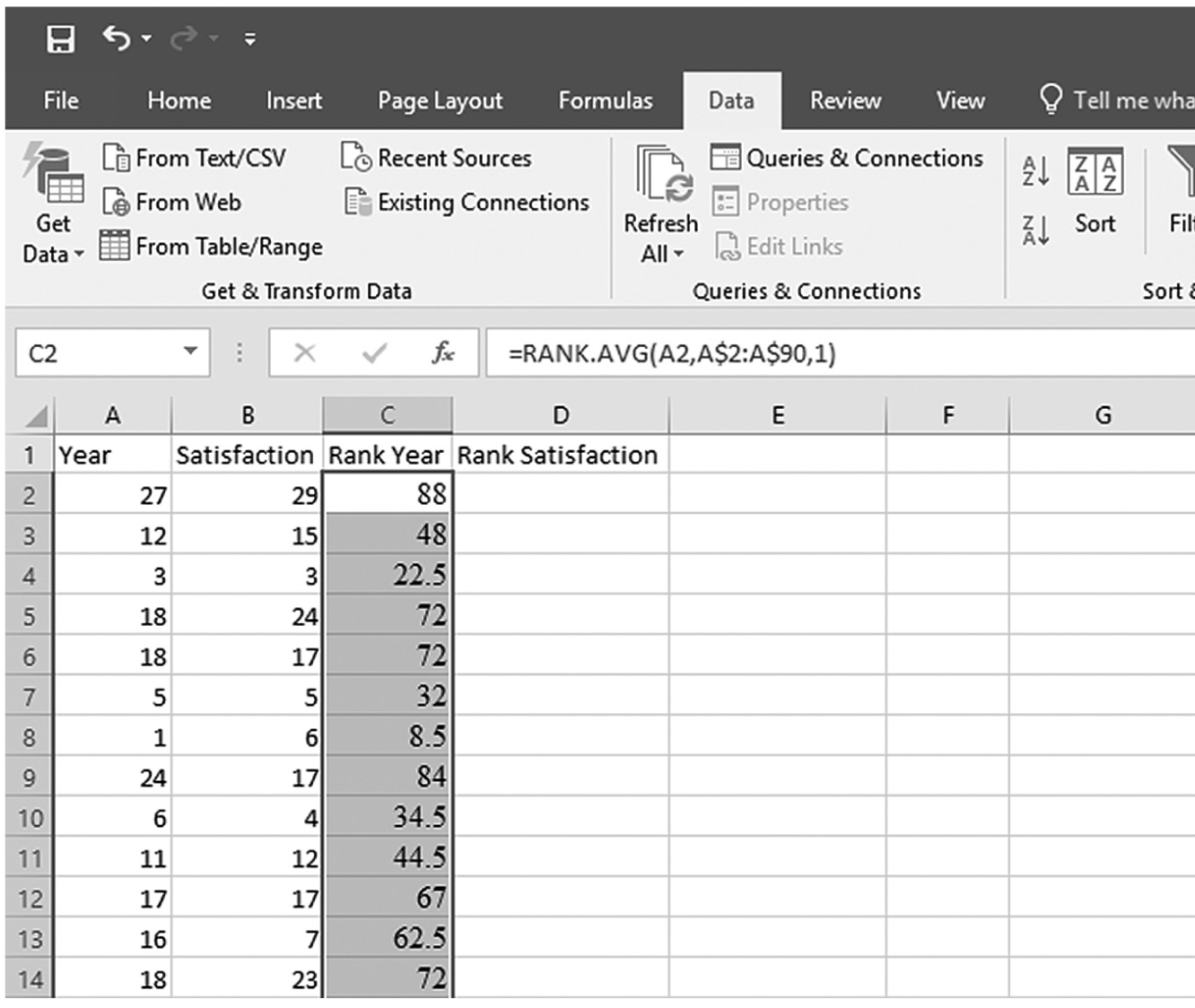
An Excel screenshot shows the entering of a function in one cell to convert raw data into rank values, and output dragged to the other cells in Column C.
Courtesy of Microsoft Excel © Microsoft 2020.
Obtaining a Spearman’s rho coefficient in Excel.
An Excel screenshot shows the Correlation coefficient
Courtesy of Microsoft Excel © Microsoft 2020.
To compute either Spearman’s rho or Kendall’s tau in SPSS, you will use NPcorrelation.sav and go to Analyze > Correlates > Bivariates, as shown in Figure 9-18. In the Bivariate Correlations dialog box, you will select the variables that you are interested in investigating the relationship between and move them over to the right window by clicking the arrow button in the middle, as shown in Figure 9-19. Pearson is checked by default in this box, but you should uncheck it and select Spearman and Kendall’s tau-b instead. Clicking “OK” will then produce the output of requested correlation coefficients. An example output is shown in Table 9-2.
Selecting Spearman’s and Kendall’s correlation coefficients in SPSS.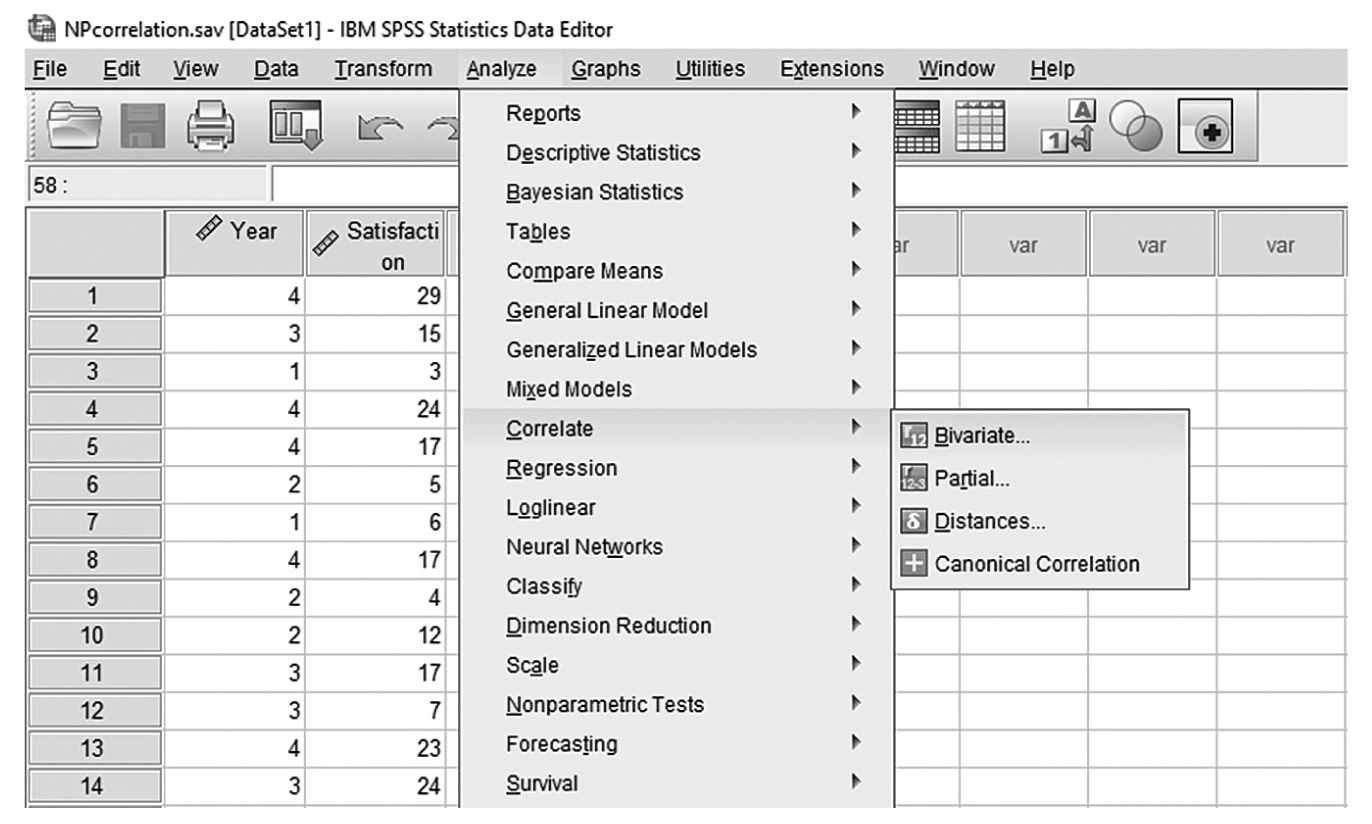
A screenshot in S P S S shows the selection of the Analyze menu, with Correlates command chosen, from which the Bivariates option is selected. The data in the worksheet has two columns of data, Year and Satisfaction, with a list of numerical data.
Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. “IBM SPSS Statistics software (“SPSS”)”. IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.
Defining variables for Spearman’s and Kendall’s correlation coefficients in SPSS.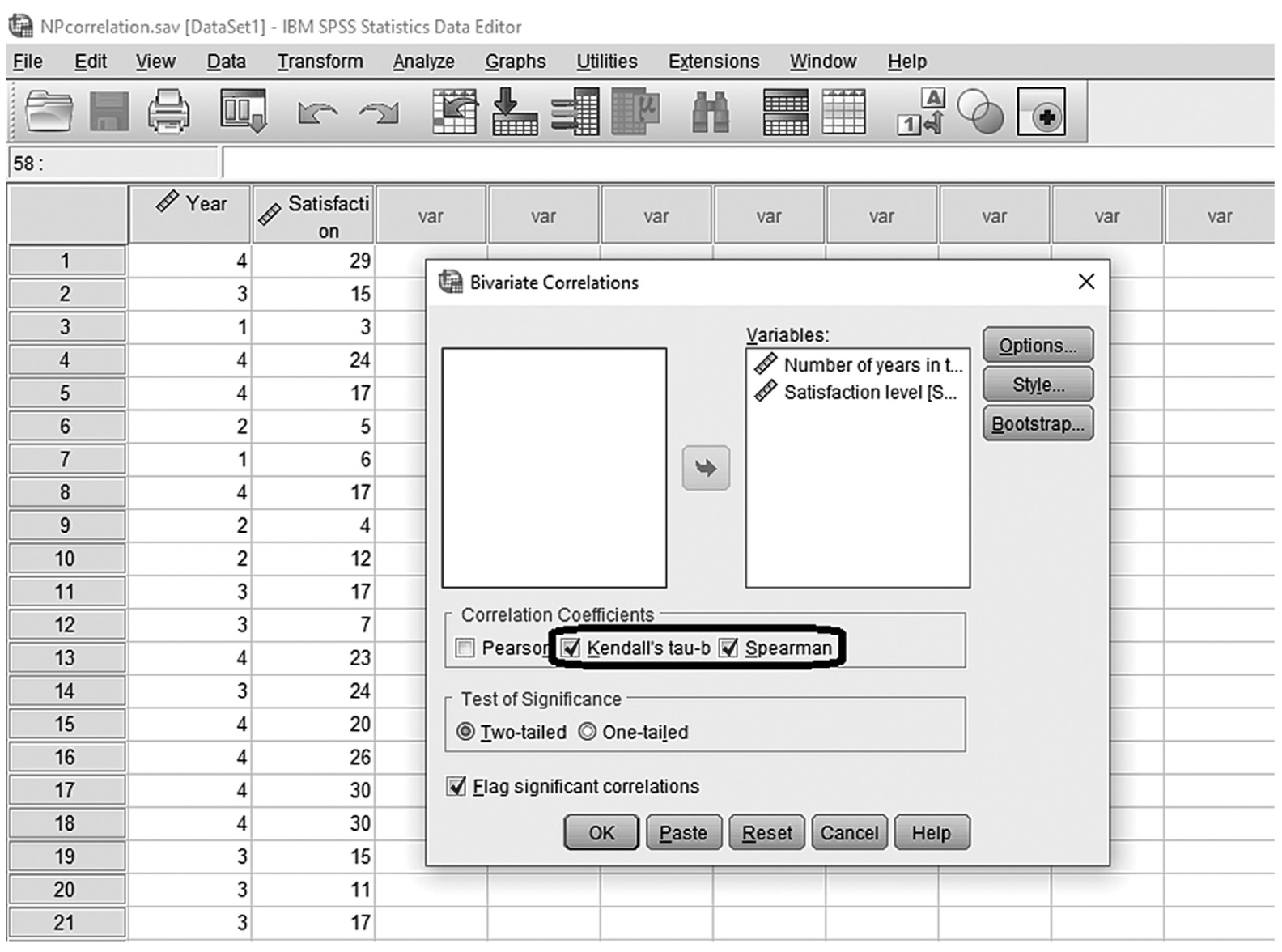
A screenshot in I B M, S P S S, Statistics Editor shows the bivariate correlations dialog box. The data in the worksheet lists numerical data under the headings, Year and Satisfaction.
Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. “IBM SPSS Statistics software (“SPSS”)”. IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.
Correlations | ||||
|---|---|---|---|---|
Satisfaction Level | Year | |||
Spearman’s rho | Satisfaction level | Correlation coefficient | 1.000 | .549** |
Sig. (two-tailed) | .000 | |||
N | 89 | 89 | ||
Year | Correlation coefficient | .549** | 1.000 | |
Sig. (two-tailed) | .000 | |||
N | 89 | 89 | ||
Kendall’s tau_b | Satisfaction level | Correlation coefficient | 1.000 | .671** |
Sig. (two-tailed) | .000 | |||
N | 89 | 89 | ||
Year | Correlation coefficient | .671** | 1.000 | |
Sig. (two-tailed) | .000 | |||
N | 89 | 89 | ||
**Correlation is significant at the 0.01 level (two-tailed)
Often there are other variables that are influencing the main relationship that you are currently investigating. If this is the case, you cannot examine the true relationship between the two variables of interest unless you control the effect of the unwanted or other variable(s) in the relationship. A partial correlation coefficient is such a measure, and it allows us to look at the true relationship between two variables after controlling for the influence of a third/unwanted variable (i.e., the effect of that variable is held constant). Let us assume that a nurse practitioner (NP) is interested in studying the relationship between a treatment and a patient outcome, but the NP believes that the level of patient anxiety is also influencing the relationship between treatment and outcome. If the NP does not control for the effect of patient anxiety, the result can be very misleading because it will not account for the true relationship between the two variables. The NP should control the effect of patient anxiety and then examine the relationship between a treatment and the patient outcome.
To explain partial correlation a bit more, let us consider Figure 9-20. The first diagram shows the relationship between patient outcome and treatment, and the second diagram shows the relationship between patient outcome and patient anxiety. When we combine those two diagrams, you will notice that the double-shaded area in the middle is the portion of variability in patient outcome that is shared by both patient anxiety and a treatment. Therefore, this is not a unique relationship between a treatment and patient outcome, and it should be removed from the rectangle of the first diagram. What is left will be the true relationship between a treatment and patient outcome.
Example diagram of partial correlation.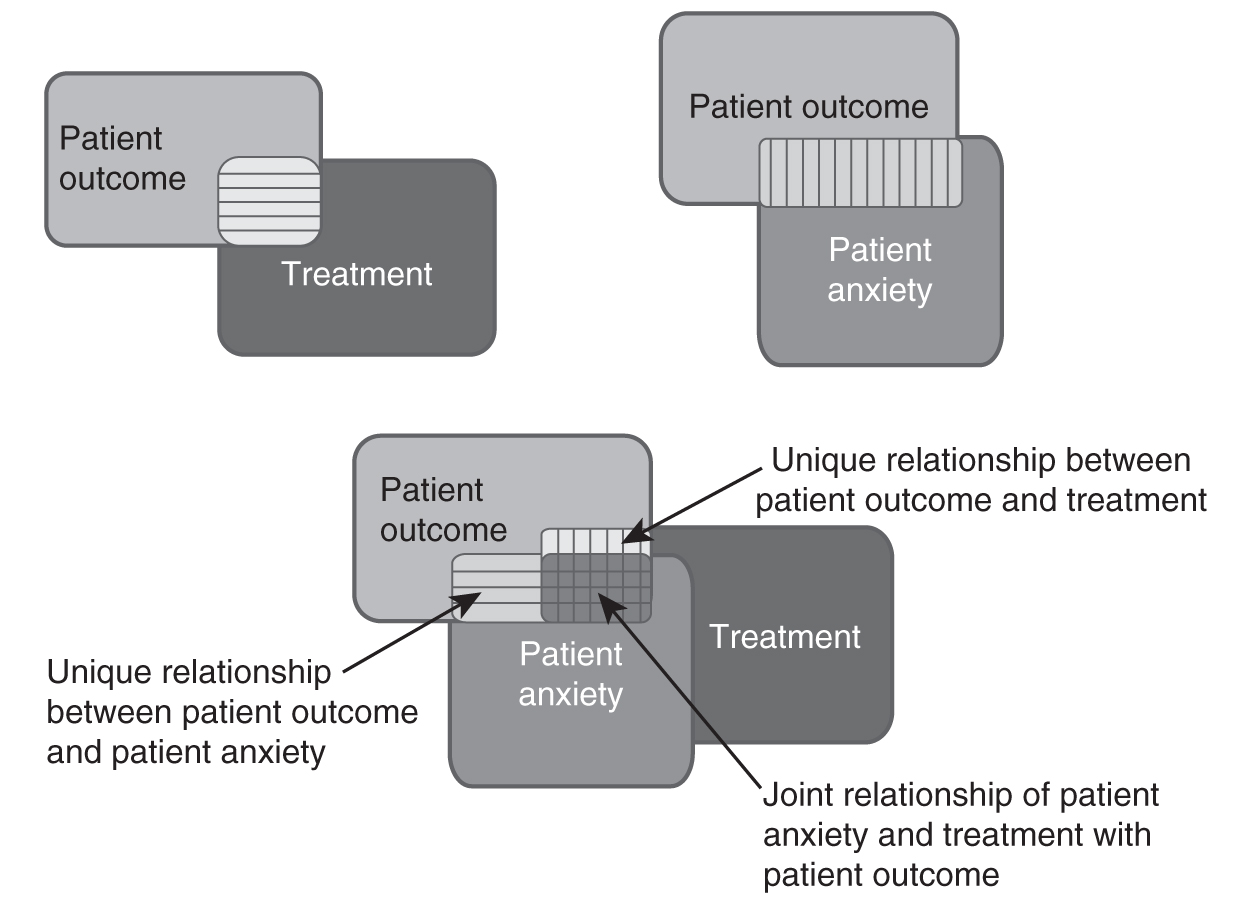
Three diagrams depict partial correlation.
To obtain a partial correlation coefficient in SPSS, you will use Partialcorrelation.sav and go to Analyze > Correlate > Partial, as shown in Figure 9-21. In the Partial Correlations dialogue box, you will select the variables you are interested in investigating a relationship between (i.e., patient outcome and treatment) and move them over to the upper window by clicking the arrow button in the middle. You will also move a variable to control (i.e., patient anxiety) to the lower window, as shown in Figure 9-22. Clicking “OK” will then produce the output of requested correlation coefficients. An example output is shown in Table 9-3.
Selecting partial correlation in SPSS.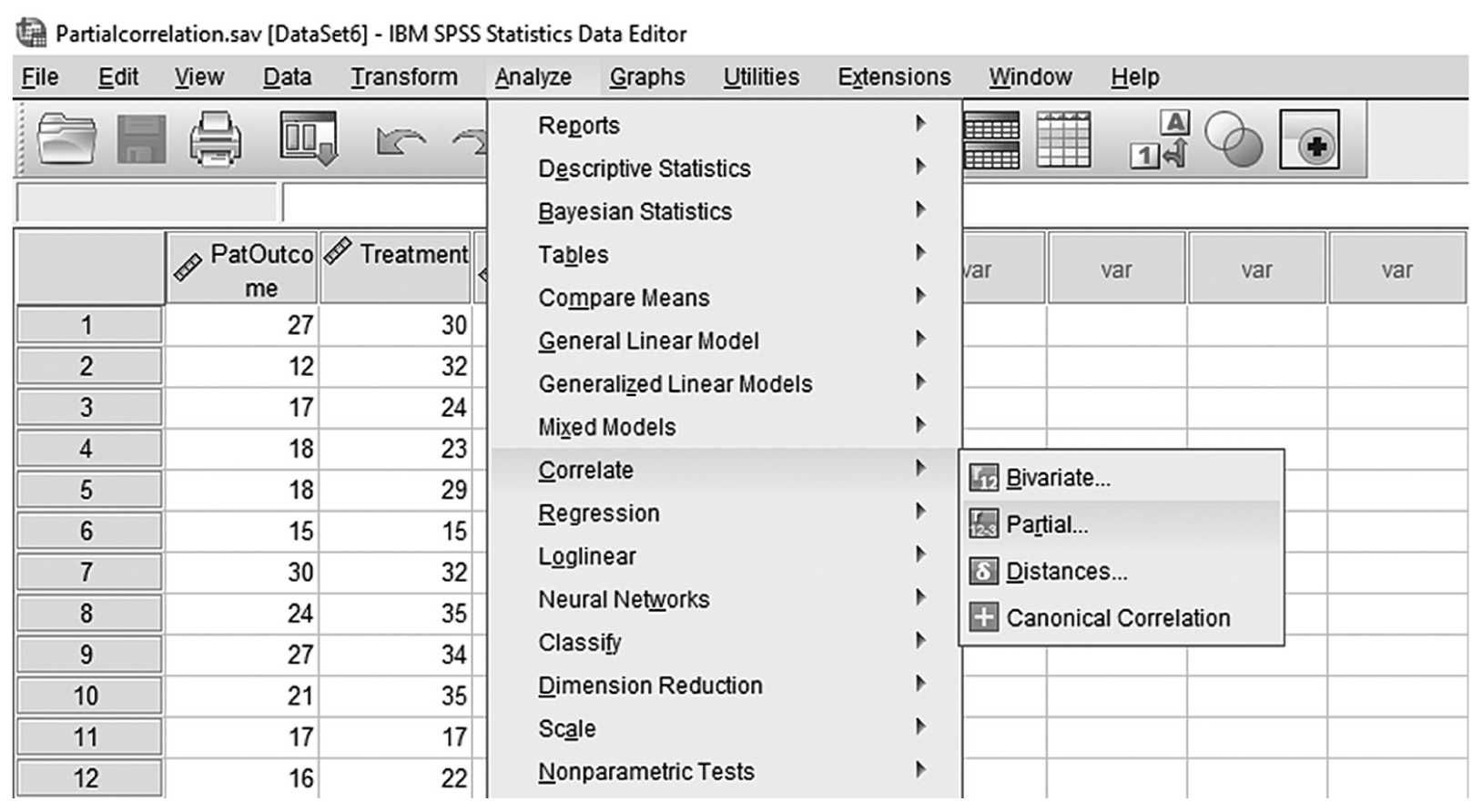
A screenshot in S P S S shows the selection of the Analyze menu, with Correlates command chosen, from which the Partial option is selected. The data in the worksheet has two columns of data, PatOutcome and Treatment, with a list of numerical data.
Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. “IBM SPSS Statistics software (“SPSS”)”. IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.
Defining the variables to compute the partial correlation coefficient in SPSS.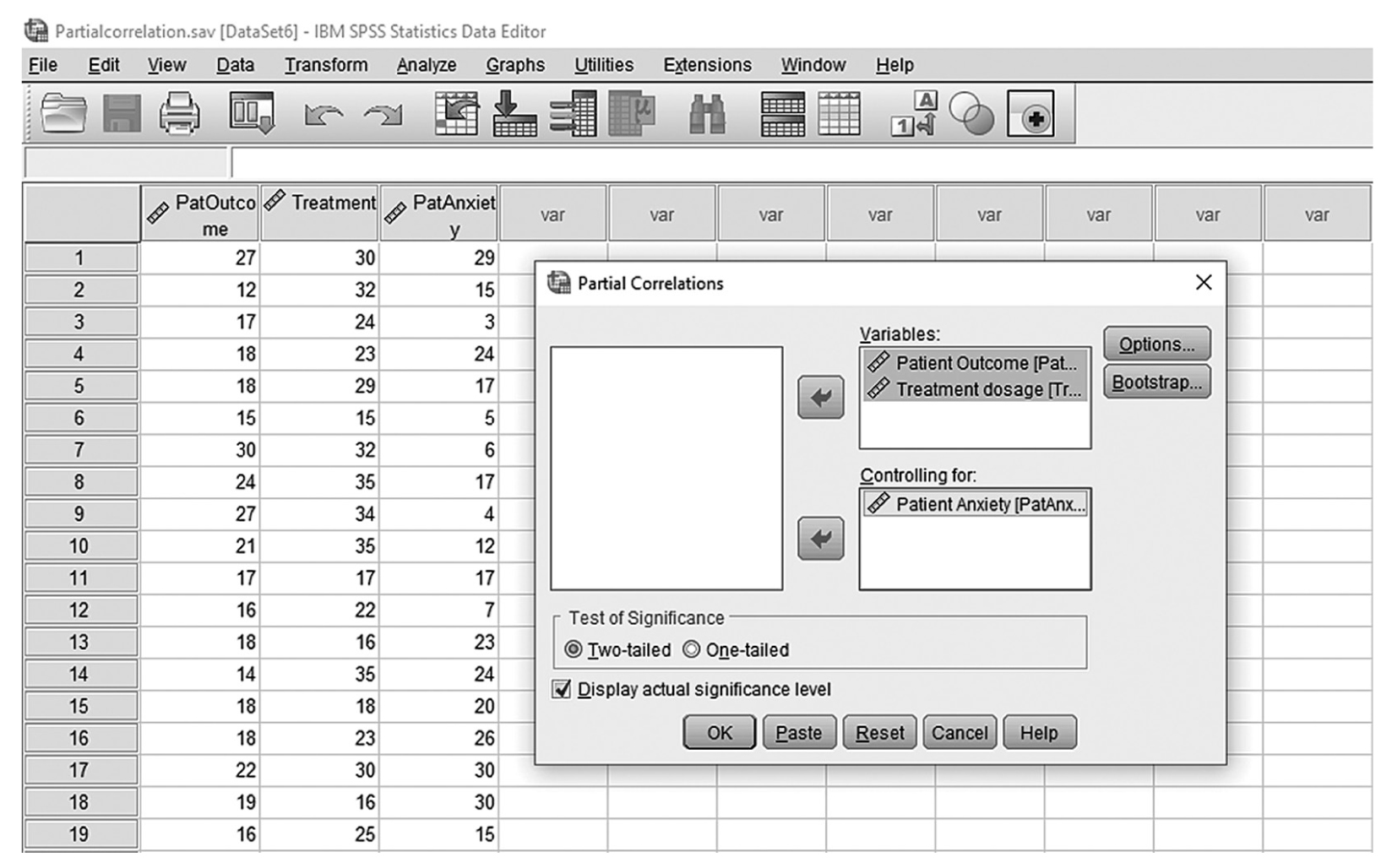
A screenshot in I B M, S P S S, Statistics Editor shows the Partial correlations dialog box. The data in the worksheet lists numerical data under the headings, PatOutcome, Treatment, and PatAnxiety.
Reprint Courtesy of International Business Machines Corporation, © International Business Machines Corporation. “IBM SPSS Statistics software (“SPSS”)”. IBM®, the IBM logo, ibm.com, and SPSS are trademarks or registered trademarks of International Business Machines Corporation.
You may recall our discussion of effect size earlier in Chapter 7 as the measure of the strength of the effect of the independent variable on the dependent variable. Correlation coefficients are commonly used measures of effect size. When using a correlation coefficient as an effect size, a value of ±.1 represents a small effect, ±.3 represents a medium effect, and ±.5 represents a large effect.
Many journals and other venues for reporting findings require a particular format intended to standardize the reporting of statistics. In nursing, we mostly use the American Psychological Association (APA) format. When reporting correlation coefficients in APA format, include the size of the relationship between variables and its associated significance. Some important things to remember when reporting correlation coefficients are: (a) you should not include a zero in front of the decimal, (b) all correlation coefficients should be reported in two decimals, and (c) the exact p-value should be reported regardless of how small or large it is. An example of reporting correlation coefficients is as follows: There was no substantial relationship between treatment dosage and surgery outcome, r = .19, p = .066, 95% CI [-.01, .40].