A decimal fraction is a proper fraction in which the denominator is a power of 10, signified by a decimal point placed at the left of the numerator. An example of a decimal fraction is 0.2, which is the same as 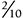 .
.
In a decimal number—for example, 2.25—the decimal point separates the whole number from the decimal fraction.
Each number or place to the left of the decimal point represents a whole number that's a power of 10, starting with ones and working up to tens, hundreds, thousand s, ten thousand s, and so on.
Each place to the right of the decimal point signifies a fraction whose denominator is a power of 10, starting with tenths and working up to hundredths, thousand ths, ten thousand ths, and so on. When working as a nurse, you'll rarely encounter decimal fractions beyond the thousand ths. (See Know your places.)
When discussing money, people use the word and to signify the decimal point, for example, saying $5.20 as “5 dollars and 20 cents.” However, when discussing decimal numbers in dosage calculations, use the word point to signify the decimal point. For example, say the number 5.2 as “5 point 2.”
![]() Memory Jogger
Memory Jogger
To remember which zeros you can safely eliminate in a decimal number, think of the letters “l” and “r” in the words left and right:
Leave a zero to the left of the decimal point if no other number appears there and you need a place holder (as in 0.5 mL). This ensures safe medication administration. (See Disappearing decimal alert.)
Remove any trailing zeros to the right of the decimal point if no other number follows and you don't need a place holder (as in 7.50 mg).
Now that you've learned the basic terms used with decimal fractions, you're ready to review the decimal calculations most often performed by nurses. But first, review these two important rules:
After performing mathematical functions with decimal numbers, you may eliminate zeros to the right of the decimal point that don't appear before other numbers. (See Zap those zeros.) In other cases, you may wish to add zeros at the end of fractions (for example, as place holders). Deleting or adding zeros at the end of a decimal fraction doesn't change the value of the number.
When writing answers to mathematical calculations and specifying drug dosages, always put a zero to the left of the decimal point if no other number appears there. This helps prevent errors. (See Disappearing decimal alert.)
Adding and subtracting decimal fractions
Before adding and subtracting decimal fractions, align the decimal points vertically to help you keep track of the decimal positions.
Placeholders, take your place
To maintain column alignment, add zeros as placeholders in decimal fractions.
Here's how to use zeros to align the decimal fractions 2.61, 0.315, and 4.8 before adding:
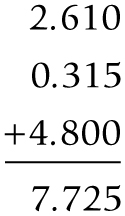

Working it out
Here are two more examples of adding and subtracting decimal fractions. First, add 0.017, 4.8, and 1.22:

Next, subtract 0.05 from 4.726:
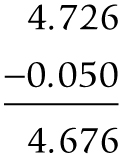
Aligning the decimal points isn't necessary before doing a multiplication problem with decimal fractions. Just leave the decimal points in their original positions and multiply the factors to find the product.
To determine where to place the decimal point in the final product, first add together the number of decimal places in both factors being multiplied. Then count out the same total number of places in the answer, starting from the right and moving to the left, and place the decimal point just to the left of the last place counted. Here's how you would multiply 2.7 and 0.81:

Multiple multiplications
Here are two more examples of multiplying decimal fractions. First, multiply 1.423 and 8.59:

Next, multiply 42.1 and 0.376:
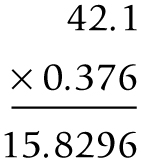

When dividing decimal fractions, align the decimal points but don't add zeros as placeholders. Remember: The number to be divided is the dividend, the number that does the dividing is the divisor, and the answer is the quotient.
Whole-number divisors
Decimal point placement is easiest when the divisor is a whole number. Just place the decimal point in the quotient directly above the decimal point in the dividend and then work the problem. For example, here's how to divide 4.68 by 2:
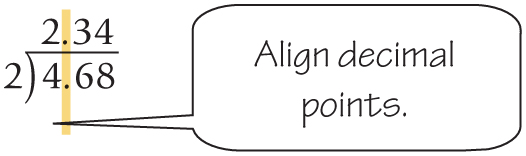
Revisiting decimal division
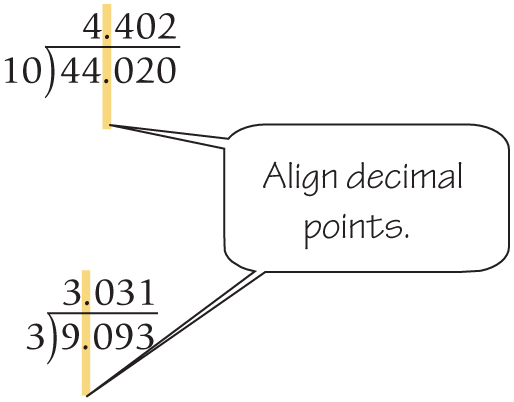
Here are two more examples of decimal point placement when the divisor is a whole number. First, divide 44.02 by 10:
Next, divide 9.093 by 3:
Decimal-fraction divisors
Of course, not every divisor is a whole number—some are decimal fractions. Dividing one decimal fraction into another requires moving the decimal points in both the divisor and the dividend. (See Dividing decimal fractions.)
Rounding off decimal fractions
Most of the instruments and measuring devices a nurse uses measure accurately only to a tenth or, at most, to a hundredth. So you'll need to round off decimal fractions—that is, convert long fractions to those with fewer decimal places. (See Remember rounding.)
Whittling decimals down
To round off a decimal fraction, follow these steps:
Suppose you want to round off the decimal fraction 0.4293. First, decide how many places to the right of the decimal point you want to keep. If you decide to round the number off to hundredths, you'll keep two places to the right of the decimal point and delete the rest (the 9 and the 3).
Now, look at the first number that you've deleted. Is this number 5 or greater than 5? If so, add 1 to the number in the hundredths place—that is, to the number 2. Your rounded-off number is now 0.43.
Suppose the number that you delete is less than 5. Then don't add 1 to the number on the left. For example, to round off 1.9085 to the nearest tenth, identify the number in the tenths position (9) and delete all the numbers to the right of it (0, 8, and 5). Because the number directly to the right of 9—the 0—is less than 5, the number 9 stays the same. The number 1.9085 rounded off to the nearest tenth is 1.9.
A practice round
Try rounding off 14.723 to the nearest hundredth:
First, decide what number is in the hundredths place (2) and delete all the numbers to the right of it (only the number 3).
Because 3 is lower than 5, you don't add 1 to the 2. So, the rounded-off number is 14.72.
WAIT!
What if you wanted to round 14.723 to the nearest tenth? Since 7 is in the tenths place, and 2 is directly to the right of it (and is less than 5), you would not add 1 to 7. So, the rounded-off number would now be 14.7.
ONE MORE TIME!
Now, round the same number 14.723 to a whole number. What number is directly to the right of 4 in the whole number 14? Since 7 is greater than 5, you would add 1 to 14, making the new rounded-off whole number 15.
See the differences in your answers depending on how you round? It's crazy!
Now, round off 0.9875 to the nearest thousand th:
The number in the thousand th place is 7. All numbers to the right of the 7—the 5—will be deleted.
Because the number to be deleted is a 5, the 7 is rounded up to 8 (7 + 1). The rounded-off number is therefore 0.988.
Again, try to round this same number 0.9875 to the nearest hundredths, tenths, and whole number. Look back at the last example if you get stuck! You can do this!
